Тема 2.5. Изгиб

Теория чистого изгиба имеет как внешнюю, так и смысловую аналогию с теорией кручения — аналогичное распределение напряжений по поперечному сече­нию: наличие опасных точек сечения, аналогичные геометрические характеристики прочности и жесткости сечения, аналогичный подход к оценке рациональности фор­мы сечения. Следует научиться строить эпюры изгибающих мо­ментов по характерным точкам и рассчитывать балки на прочность.

Вопросы для самоконтроля

1. В каком случае балка работает на изгиб?

2. Что такое чистый и поперечный изгиб? Какие внутренние силовые факторы возникают в поперечных сечениях бруса в этих случаях?

3. Каким методом определяют внутренние силовые факторы, действующие в поперечных сечениях на изгиб?

4. Чему равна поперечная сила и изгибающий момент в произвольном сечении балки при изгибе?

5. Для чего строятся эпюры поперечных сил и изгибающих моментов?

6. Сформулируйте правило знаков для поперечной силы и изгибающего мо­мента.

7. Как меняется характер эпюр поперечных сил и изгибающих моментов в точ­ках приложения сосредоточенных, сил и моментов?

8. Напишите формулы для определения осевых моментов сопротивления при изгибе для прямоугольника, круга и кольца.

9. Изгиб прямого бруса.

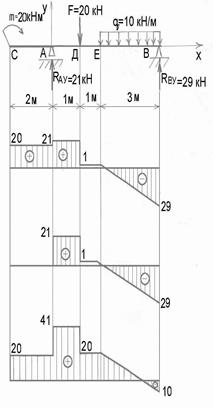
1 Для какого варианта эпюра поперечных сил построена верно?

2 На каком участке бруса эпюра изгибающих моментов имеет вид квадратной параболы?

В результате изучения темы студент должен:

иметь представлениео дифферинциальных зависимостях при изгибе; линейных и угловых перемещениях; жесткости при изгибе;

знатьвиды изгиба и внутренние силовые факторы; правила построения и контроля эпюр поперечных сил и изгибающих моментов; распределение нормальных напряжений по сечению при изгибе; условия прочности;

уметьстроить эпюры поперечных сил и изгибающих моментов по длине балок; выполнять расчеты балок на прочность по предельному состоянию.