Механические системы
Фазовыми переменными в механических поступательных системах являются силы и скорости. Используют одну из двух возможных электромеханических аналогий. В дальнейшем будем использовать ту из них, в которой скорость относят к фазовым переменным типа потенциала, а силу считают фазовой переменной типа потока. Учитывая формальный характер подобных аналогий, в равной мере можно применять и противоположную терминологию.
Компонентное уравнение, характеризующее инерционные свойства тел, в силу второго закона Ньютона имеет вид:
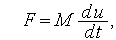
| (8) |
где 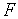 — сила;
— сила; 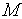 — масса;
— масса; 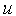 — поступательная скорость.
— поступательная скорость.
Упругие свойства тел описываются компонентным уравнением, которое можно получить из уравнения закона Гука. В одномерном случае (если рассматриваются продольные деформации упругого стержня):
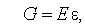
| (9) |
где 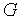 — механическое напряжение;
— механическое напряжение;  — модуль упругости;
— модуль упругости; 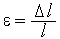 — относительная деформация;
— относительная деформация; 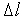 — изменение длины
— изменение длины 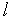 упругого тела под воздействием
упругого тела под воздействием 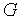 . Учитывая, что
. Учитывая, что 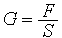 , где
, где 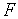 — сила,
— сила, 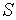 — площадь поперечного сечения тела, и дифференцируя (9), имеем:
— площадь поперечного сечения тела, и дифференцируя (9), имеем:
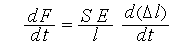
или
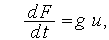
| (10) |
где 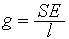 — жесткость (величину, обратную жесткости, называют гибкостью
— жесткость (величину, обратную жесткости, называют гибкостью 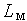 ),
), 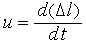 — скорость.
— скорость.
Диссипативные свойства в механических системах твердых тел выражаются соотношениями, характеризующими связь между силой трения и скоростью взаимного перемещения трущихся тел, причем в этих соотношениях производные сил или скоростей не фигурируют, как и в случае описания с помощью закона Ома диссипативных свойств в электрических системах.
Топологические уравнения характеризуют, во-первых, закон равновесия сил: сумма сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера), во-вторых, закон скоростей, согласно которому сумма относительной, переносной и абсолютной скоростей равна нулю.
В механических вращательных системах справедливы компонентные и топологические уравнения поступательных систем с заменой поступательных скоростей на угловые, сил — на вращательные моменты, масс — на моменты инерции, жесткостей — на вращательные жесткости.
Условные обозначения простых элементов механической системы показаны на рис. 1,б.
Нетрудно заметить наличие аналогий между электрической и механической системами. Так, токам и напряжениям в первой из них соответствуют силы (либо моменты) и скорости механической системы, компонентным уравнениям (4) и (5) и фигурирующим в них параметрам 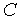 и
и 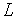 — уравнения (8) и (10) и параметры
— уравнения (8) и (10) и параметры 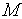 и
и 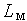 , очевидна аналогия и между топологическими уравнениями. Далее параметры
, очевидна аналогия и между топологическими уравнениями. Далее параметры 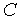 и
и 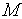 будем называть емкостными (емкостного типа), параметры
будем называть емкостными (емкостного типа), параметры 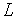 и
и 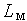 — индуктивными (индуктивного типа), а параметры
— индуктивными (индуктивного типа), а параметры 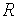 и
и 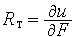 — резистивными (резистивного типа).
— резистивными (резистивного типа).
Имеется и существенное отличие в моделировании электрических и механических систем: первые из них одномерны, а процессы во вторых часто приходится рассматривать в двух- (2D) или трехмерном (3D) пространстве. Следовательно, при моделировании механических систем в общем случае в пространстве 3D нужно использовать векторное представление фазовых переменных, каждая из которых имеет шесть составляющих, соответствующих шести степеням свободы.
Однако отмеченные выше аналогии остаются справедливыми, если их относить к проекциям сил и скоростей на каждую пространственную ось, а при графическом представлении моделей использовать шесть эквивалентных схем — три для поступательных составляющих и три для вращательных.
Дата добавления: 2015-08-01; просмотров: 1170;
