Исходные уравнения для формирования моделей на макроуровне

Исходное математическое описание процессов в объектах на макроуровне представлено системами обыкновенных дифференциальных и алгебраических уравнений. Аналитические решения таких систем при типичных значениях их порядков в практических задачах получить не удается, поэтому в САПР преимущественно используются алгоритмические модели. В этом параграфе изложен обобщенный подход к формированию алгоритмических моделей на макроуровне, справедливый для большинства приложений.

Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения.

Компонентными уравнениями называют уравнения, описывающие свойства элементов (компонентов), другими словами, математическая модель элемента (ММЭ) представляется компонентными уравнениями.

Топологические уравнения описывают взаимосвязи в составе моделируемой системы.

В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы (ММС).

Очевидно, что компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях компонентных и топологических уравнений. Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов. Наличие аналогий приводит к практически важному выводу: значительная часть алгоритмов формирования и исследования моделей в САПР оказывается инвариантной и может быть применена к анализу проектируемых объектов в разных предметных областях. Единство математического аппарата формирования ММС особенно удобно при анализе систем, состоящих из физически разнородных подсистем.

В перечисленных выше приложениях компонентные уравнения имеют вид:

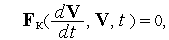
(1)

топологические уравнения:

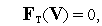
(2)

где 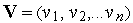— вектор фазовых переменных, 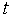— время.

Различают фазовые переменные двух типов, их обобщенные наименования — фазовые переменные типа потенциала(например, электрическое напряжение) и фазовые переменные типа потока (например, электрический ток). В стандарте VHDL AMS их называют соответственно переменными across quantity, вторые — through quantity. Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение — связи между однотипными фазовыми переменными в разных компонентах.

Модели можно представлять в виде систем уравнений или в графической форме, если между этими формами установлено взаимно однозначное соответствие. В качестве графической формы часто используют эквивалентные схемы.

Ниже рассмотрим примеры компонентных и топологических уравнений для разных типов систем.