Примеры. 1. Реализовать в Excel вычисление суммы двух матриц размерностью 2×3.

1. Реализовать в Excel вычисление суммы двух матриц размерностью 2×3.

Суммой матриц А и В одной и той же размерности n×m называется матрица С той же размерности такая, что

c_ik = a_ik + b_ik.

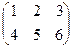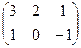Для проверки правильности реализации вычисления суммы матриц в Excel целесообразно рассмотреть контрольный пример. Пусть даны две матрицы размерности 2×3: А = и В = . Найти их сумму – матрицу С = А + В.

Вычислим значения элементов матрицы С «вручную», чтобы затем сравнить их с машинным вариантом.

С =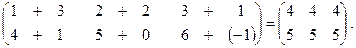

Реализуем вычисление суммы матриц в Excel. Для этого:

- Откройте лист рабочей книги и дайте ему имя «Операции с матрицами 1».

- Введите в ячейки А1, Е1, I1 соответственно пояснения: Матрица А, Матрица В, Матрица С.

- Введите в блок ячеек А3:С4 элементы матрицы А, а в блок ячеек Е3:G4 элементы матрицы B.

- Блок ячеек I3:K4 используйте для вычисление элементов матрицы С (как показано в режим показа формул рисунок 217).

Рисунок 217

- В ячейку I3 введите формулу =А3+Е3. Для ввода адресов ячейки в формулу используйте мышь. Для этого: активизируйте ячейку I3, введите знак «равно» (=), щелкните по ячейке А3, введите знак «плюс» (+), щелкните по ячейке Е3. Это поможет избежать неверного введения адресов ячеек.

- Оставьте адреса А3 и Е3 относительными.

- Скопируйте содержимое ячейки I3 в блок ячеек J3:K3, используя маркер заполнения. При копировании по строке относительные адреса столбцов в формуле поменяются, а относительные номера строк останутся неизменными, что нам и нужно для реализации решения поставленной задачи.

- Скопируйте содержимое ячейки I3 в ячейку I4. При копировании по столбцу имя столбца не изменится, а номера строки изменятся, что нас устраивает.

- Скопируйте содержимое ячейки I4 в блок ячеек J4:K4. При копировании по строке относительные адреса столбцов поменяются, а относительные номера строк останутся неизменными, что нам и нужно.

В результате получим значения элементов матрицы С как показано на рисунке 218.

Рисунок 218

Решение, полученное в Excel, совпадает с «ручным» счетом, значит, реализация решения задачи сделана верно и может быть использована для вычисление суммы любых двух матриц размерности 2×3.

Вычислите сумму двух матриц: А = 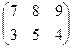, В = 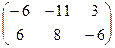, используя имеющуюся таблицу. Для этого введите в блоки ячеек А3:С4 и Е3:G4 новые значения элементов матриц А и B. Тогда в блоке ячеек I3:K4 получите новые значения элементов матрицы С как показано в режиме решения на рисунке 219.

Рисунок 219

2. Реализовать в Excel вычисление произведения матрицы размерности 2×3 на число.

Произведением матрицы А на число λ (или числа λ на матрицу А) называется матрица В такая, что

b_ik = λ∙a_ik,

т.е. при умножении матрицы на число (или числа на матрицу) надо все элементы матрицы умножить на это число.

Рассмотрим контрольный пример. Пусть дана матрица размерностью 2×3: А = 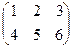и число λ = 10. Вычислим матрицу В1.

Реализуйте вычисление произведения матрицы размерности 2×3 на число в Excel. Для этого:

- Откройте лист рабочей книги «Операции с матрицами 1».

- В ячейку D6 введите число 10. В ячейку С6 – пояснительный текст λ =.

- В блок ячеек А9:С10 введите формулы для вычисления произведения матрицы на число. Для этого:

- В ячейку А9 введите формулу =А3*D6 и нажмите кнопку F4, чтобы сделать адрес D6 абсолютным. Получится формула =А3*$D$6.

- Скопируйте содержимое ячейки А9 в блок ячеек В9:С9. Относительный адрес при копировании изменится (поменяется имя столбца), а абсолютный останется неизменным, что нас устраивает.

- Скопируйте содержимое ячейки А9 в ячейку А10. Относительный адрес при копировании изменится (поменяется номер строки), а абсолютный останется неизменным, что нам и надо.

- Скопируйте содержимое ячейки А10 в блок ячеек В10:С10. Относительные адреса при копировании изменятся, а абсолютные нет – как показано в режиме формул на рисунке 220. В режиме решения таблица будет иметь вид рисунок 221.

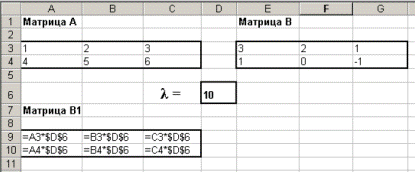
Рисунок 220

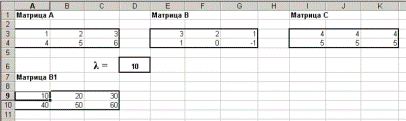
Рисунок 221

3. Реализовать в Excel вычисление произведения матрицы А размерности 3×3 на вектор-столбец Х.

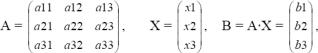
где

b₁ = a₁₁∙b₁ + a₁₂∙b₂ + a₁₃∙b₃,

b₂ = a₂₁∙b₁ + a₂₂∙b₂ + a₂₃∙b₃,

b₃ = a₃₁∙b₁ + a₃₂∙b₂ + a₃₃∙b₃.

Рассмотрим контрольный пример.

Пусть матрица А = 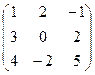, вектор-столбец Х = 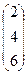. Для вычисления вектора В = А∙Х воспользуемся формулами, вычисляющими значения b_i:

b₁ = 1∙2 + 2∙4 + (–1)∙6 = 4,

b₂ = 3∙2 + 0∙4 + 2∙6 = 18,

b₃ = 4∙2 + (–2)∙4 + 5∙6 = 30.

Реализуем вычисление произведения матрицы А размерностью 3×3 на вектор-столбец Х в Excel. Для этого:

- Откройте лист рабочей книги и дайте ему имя «Операции с матрицами 2».

- Введите в ячейки А1, Е1, C6 соответственно пояснения: Матрица А, Вектор-столбец X, Произведение А∙Х.

- Введите в блок ячеек А2:С4 элементы матрицы А, а в блок ячеек Е2:Е4 элементы вектор столбца Х. В блоке ячеек D7:D9 организуйте вычисление элементов матрицы B – как показано в режиме показа формул на рисунке 222. Для этого:

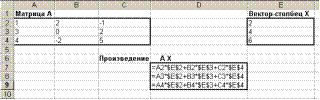
Рисунок 222

- В ячейку D7 введите формулу =А2*$Е$2+В2*$Е$3+С2*$Е$4. Адреса ячеек блока Е2:Е4 взять абсолютными, чтобы при копировании они не менялись.

- Скопируйте содержимое ячейки D7 в блок ячеек D8:D9. Относительные адреса ячеек подстроятся под нужные нам формулы.

Получим таблицу, представленную на рисунке 223 (в режиме решения).

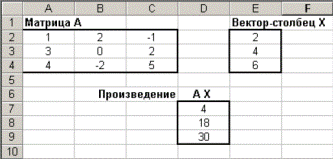
Рисунок 223