Погрешности измерения. Правила записи результатов измерений

1. Погрешности измерения. Любое экспериментальное измерение физической величины может быть произведено не «абсолютно точно», а лишь с точностью до гарантированной данным экспериментом величины погрешности.

2. Истинное значение измеряемой величины. Чаще всего в качестве истинного значения в измерениях выступает:

– либо теоретически введенная идеальная величина;

– либо справочное значение величины, определенное более точными экспериментальными средствами, чем данный эксперимент;

– либо среднее значение, вычисленное в данном эксперименте.

3. Типы (классы) погрешностей.

По «происхождению» и характеру проявления погрешности делятся на промахи, систематические и случайные.

Промахи (по другой терминологии – недостоверные измерения) совершаются чаще всего из-за неопытности экспериментатора и их нельзя учесть каким-то научно определенным способом. К счастью, промахи обычно резко выпадают из «правильных» значений измерений и поэтому сравнительно легко исключаются.

Систематические погрешности проистекают в общем случае из трех источников: 1) погрешности измерительных приборов ( приборные погрешности); 2) систематические погрешности методики измерения; 3) неполное знание о природе самой измеряемой величины.

Случайные погрешности – погрешности, обусловленные случайным изменением самой измеряемой величины, условий измерения (среды измерения) или случайными воздействиями на измерительные приборы.

По форме отображения погрешности делят на абсолютные и относительные.

Абсолютная погрешность ∆Х выражается разностью между измеренным Х' и истинным Х значением величины и вносится в результат измерения в тех же единицах, что и сама величина:

∆Х = Х' – Х,

Например: Запись результата измерения в данной точке: ∆I = 14,5 – 13,6 = 0,9 мА.

Относительная погрешность – отношение абсолютной погрешности к истинному значению:

δХ = ∆Х/Х.

Пример: δI = 0,9/13,6 = 0,066.

Относительную погрешность более удобно выражать в процентах (процентная погрешность):

δХ % = (∆Х/Х)·100 %.

Пример: δI = 6,6 %.

Определение приборной погрешности производится по классу точности использованных приборов.

Поскольку относительная погрешность электроизмерительного прибора - переменная величина, она не может применяться в качестве характеристики точности прибора. Для характеристики точности стрелочных приборов вводят приведенную погрешность.

Приведенная погрешность Епр – отношение максимальной абсолютной погрешности измерения к пределу измерения Хmах, выраженное в процентах:

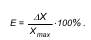
G = (∆Хmax/Хmax)·100.

Например, если абсолютная погрешность амперметра ∆X = 0,1 А, а предел измерения этого амперметра Хmах = 10 А, то Епр = (0,1/10)*100% = 1%.

По величине приведенной погрешности все электроизмерительные приборы относят к определённому классу точности. Существует восемь классов точности электроизмерительных приборов: 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Показатель класса точности определяет приведенную погрешность прибора в процентах.

Так, амперметр класса точности 1,5 с пределом измерения 5 А имеет в любом месте шкалы абсолютную погрешность ∆X = 0,015*5 = 0,075 А.

Класс точности прибора указывается на шкале. Приборы без указания класса точности имеют точность ниже 4% и называются индикаторными, а не измерительными.