Теория производства и предельных продуктов. Закон убывающей предельной производительности факторов производства. Эффект масштаба

Теория производства изучает зависимость между количеством исполь­зуемых ресурсов и объемами выпускаемой продукции. В основе этой тео­рии лежит концепция производственной функции.

Производственная функция определяет максимальный объем вы­пуска продукции при каждом заданном количестве ресурсов.Эта функция описывает зависимость между затратами ресурсов и выпуском продук­ции, позволяя определить максимально возможный объем выпуска продук­ции при каждом заданном количестве ресурсов, или минимально возмож­ное количество ресурсов для обеспечения заданного объема выпуска про­дукции. Производственная функция суммирует только технологически эф­фективные приемы комбинирования ресурсов для обеспечения максималь­ного выпуска продукции. Любое усовершенствование в технологии произ­водства, способствующее росту производительности труда, обусловливает новую производственную функцию.

Подзатратами понимается все, что производитель (фир­ма) закупает для использования в целях достижения необходимого результата.Выпуском может быть любое благо (продукция или услуга), изготовленное фирмой для продажи.

Деятельность фир­мы можно обозначать как производственную, так и коммерческую деятельность, например транспортировку, хранение и даже покуп­ку продукции с целью ее последующей перепродажи. Экономическая деятельность фирмы может быть описана про­изводственной функцией:

Q = f (F₁, F₂, .... F_n),

где: Q – максимальный объем производства при заданных затратах; F₁ – количество использованного фактора f₁; F₂ – количество использованного фактора f₂; F_n – количество использованного фактора f_n.

При изучении производственной функции необходимо подробнее рас­смотреть категории эффекта масштаба производстваи отдачи от фактора.

Масштаб производства задается производственной функцией. Если фирма принимает решение об одновременном и про­порциональном изменении количества всех применяемых факторов, то на­лицо – изменение масштаба производства.

Предположим, что фирма, имеющая первоначально объем выпуска про­дукции Q₁, принимает решение об увеличении масштаба производства в n раз. В этом случае заданная производственная функция примет следующий вид: Q₂ = f (nL, nK),

где: Q₂ – объем выпуска после изменения масштаба производства.

Взаимосвязь между изменением масштаба производства и соответствующим изменением в объеме выпуска продукции называется отда­чей от масштаба.Отдачу от масштаба можно измерить путем сравнения процентного изменения в выпуске продукции с процентным изменением в количестве всех применяемых факторов.

Принято различать:

– постоянная отдача от масштаба.Если при пропорциональном увели­чении количества факторов в n раз, объем производства тоже возрастет в n раз, то имеет место постоянная отдача от масштаба, т.е. Q₂ = nQ₁ (где Q₁ – первоначальный объем производства);

– возрастающая отдача от масштаба.В случае, когда пропорциональ­ное увеличение количества всех применяемых факторов в n раз вызовет рост объема производства больше, чем в n раз, наблюдается возрастающая отдача от масштаба, т.е. Q₂ > nQ₁;

– уменьшающаяся отдача от масштаба.Когда пропорциональное уве­личение всех применяемых факторов в n раз вызывает рост объема произ­водства меньше, чем в n раз, имеет место убывающая отдача от масштаба, т.е. Q₂ < nQ₁.

Отдача от фактора показывает зависимость между объемом выпус­каемой продукции и изменениями в количестве одного фактора при неизменном количестве другого.По мере наращивания одного перемен­ного фактора начинает проявляться тенденция, известная как закон убыва­ющей предельной производительности, или убывающей предельной доход­ности фактора производства.

Закон убывающей предельной производительности.Предположим сначала, что F₁ является переменным фактором, тогда как остальные (n – 1) факторов (F₂, ….. F_n) постоянны:

Q = f (F₁, F₂, … F_n),

где:F₂, … F_n = const.

Для того чтобы отразить влияние переменного фактора на про­изводство, вводятся понятия совокупного (общего), среднего и пре­дельного продукта.

Совокупный продукт (ТР) – это количество эко­номического блага, произведенное с использованием некоторого ко­личества переменного фактора.

Разделив совокупный продукт на израсходованное количество переменного фактора, можно получить средний продукт (AP): АР = Q / F.

Предельный продуктобычно определя­ется как прирост совокупного продукта, полученный в резуль­тате бесконечно малых приращений количества использованного переменного фактора:

MP = DQ / DF.

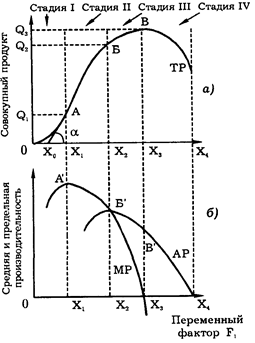Совокупный продукт (Q) с ростом использования в производ­стве переменного фактора (F₁) будет увеличиваться, однако этот рост имеет определенные пределы в рамках заданной технологии (рис.).

На первой стадии производства (0А)увеличение затрат труда способствует все более полному исполь­зованию капитала: предельная и общая производительность труда растут. Это выражается в росте предельного и среднего продукта, при этом МР > АР (рис. (б)). В точке А' предельный продукт достигает своего максимума.

На второй стадии (АБ) величина пре­дельного продукта уменьшается и в точке Б' становится равной среднему продукту (МР = АР). Если на первой стадии (0А) сово­купный продукт возрастает медленнее, чем использованное количе­ство переменного фактора, то на второй стадии (АБ) совокупный про­дукт растет быстрее, чем использованное количество переменного фактора (рис. (а)).

На третьей стадии производства (БВ) МР < АР, в результате чего совокупный продукт растет медленнее затрат переменного фактора и, наконец, наступает четвертая стадия (пос­ле точки В), когда МР < 0. В результате прирост переменного фак­тора F₁ приводит к уменьшению выпуска совокупной продукции (конечно, при условии, что все единицы переменного фактора каче­ственно однородны и добавление все новых и новых единиц не ве­дет к качественному изменению технологии).

В этом и заключается закон убывающей предельной производительности. Он утверждает, что с ростом исполь­зования какого-либо производственного фактора (при неизменнос­ти остальных) рано или поздно достигается такая точка, в которой дополнительное применение переменного фактора ведет к снижению относительно и далее абсолютного объемов выпуска продук­ции. Увеличение использования одного из факторов (при фиксиро­ванности остальных) приводит к последовательному снижению от­дачи его применения.

Закон убывающей предельной производительности носит не абсолютный, а относительный характер. Во-первых, он применим лишь на краткосрочном отрезке времени, когда хотя бы один из факторов производства остается неизменным. Во-вторых, техни­ческий прогресс постоянно раздвигает его границы.

Правило наименьших издержек.Равновесие производителя обеспечивается тогда, когда он достигает максимума производства, точно так же, как и потреби­тель оказывается в положении равновесия, когда максимизирует свое благосостояние (удовольствие от потребляемых благ).

MRP₁ / P₁ = MRP₂ / P₂ = … = MRP_n / P_n,

где: MRP – предельный продукт в денежном выражении.

Правило наименьших издержек –этоусловие, согласно которому издержки мини­мизируются в том случае, когда последний доллар (марка, рубль и так далее), затраченный на каждый ресурс, дает одинаковую отдачу – одинаковый предельный продукт.

Правило наименьших издержек обеспечивает равновесие положения производителя. Когда отдача всех факторов одинакова, задачаих перераспре­деления отпадает, так как уже нет ресурсов, которые приносят больший доход по сравнению с другими. Производитель находится в положении равновесия. В этом положении достигается оптимальная комбинация факторов производства, обеспечивающая максимизацию издержек.

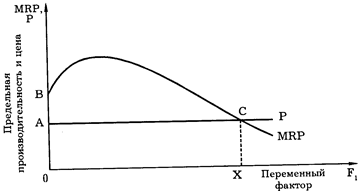Правило максимизации прибыли.При совершенной конкуренции цены благ и цены ресурсов являются заданными, независимыми от данного производителя ве­личинами. Отсюда можно сделать вывод, что предельная произво­дительность какого-либо ресурса в денежном выражении будет иметь ту же динамику изменения, что и предельная производи­тельность в натуральном («физическом») выражении, поскольку, чтобы получить первую, достаточно вторую умножить на постоян­ную цену. Ресурс поэтому будет находить применение в производ­стве до тех пор, пока его предельная производительность в денеж­ном выражении будет не ниже его цены (рис.). Это означает, что цена ресурсов измеряет предельную производитель­ность этих факторов. Если цена ресурсов равна Р, а кривая ВС является стоимостным выражением предельной производительности MRP, то производство будет продолжаться до тех пор, пока MRP не будет равно Р (см. рис.). В этом случае производитель будет максимизировать свой доход.

Правило максимизации прибыли является дальнейшим раз­витием правила минимизации издержек. Оно утверждает, что это соотноше­ние равно единице для всех i = 1, 2,..., n:

MRP₁ / P₁ = MRP₂ / P₂ = MRP_n / P_n = 1.