Кинетического момента СМТ

Запишем теорему об изменении момента количества движения МТ (1.34) для n-й точки СМТ, учтя, что на нее действуют 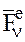– равнодействующая всех внешних сил и 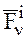– равнодействующая всех внутренних сил:

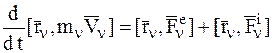. (n=1,2,...,n)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

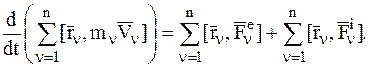(4.21)

Используя формулу для главного момента системы сил (Ч.2 Статика) и учтя свойство внутренних сил – соотношение (3.3), имеем:

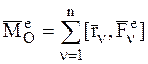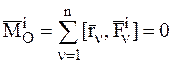, , (4.22)

где 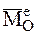- главный момент всех внешних сил, а 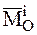- главный момент всех внутренних сил относительно какого-либо центра.

Введем понятие кинетического момента СМТ относительно какого-либо центра О.

Определение: Кинетическим моментом или моментом количества движения СМТ называется геометрическая сумма моментов количества движения МТ, входящих в СМТ, относительно того же центра:

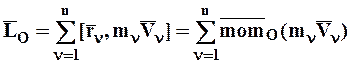. (4.23)

Подставив (4.22) и (4.23) в (4.21), получим теорему об изменении кинетического момента СМТ в следующем виде:

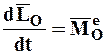. (4.24)

Теорема: Производная по времени от кинетического момента СМТ относительно какого-либо центра равна главному моменту всех внешних сил, действующих на СМТ, относительно того же центра.

Спроектировав соотношения (4.24) на оси декартовой системы координат с началом в центре О и учтя связь между моментами силы относительно точки и оси, получим:

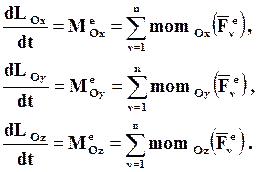(4.25)

Отсюда следует, что производная по времени от проекции кинетического момента СМТ на какую-либо ось равна проекции главного момента всех внешних сил, действующих на СМТ, на эту ось или сумме моментов всех внешних сил, действующих на СМТ, относительно этой оси.

Следствия:

· Если 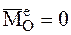, то из соотношения (4.24) следует, что

.

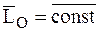Если главный момент внешних сил, действующих на СМТ, относительно какого-либо центра равен нулю, то кинетический момент СМТ относительно того же центра постоянен по величинеи направлению и равен кинетическому моменту СМТ относительно того же центра в начальный момент времени:

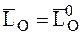. (4.26)

Соотношение (4.26) выражает закон сохранения кинетического момента для СМТ.

· Если 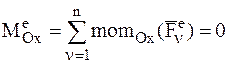(для определенности выбрана ось х), то из первого соотношения (4.25) следует, что

.

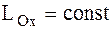Если проекция главного момента всех внешних сил, действующих на СМТ, на какую-либо ось (сумма моментов всех внешних сил относительно какой-либо оси) равна нулю, то проекция кинетического момента на эту ось является постоянной величиной и равняется проекции кинетического момента на эту ось в начальный момент времени

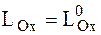. (4.27)

Найдем кинетический момент НМС, вращающейся относительно неподвижной оси Оz (рис. 33)

.

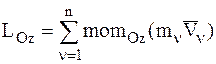Скорость n-й точки НМС, вращающейся относительно неподвижной оси, определится соотношением (Ч.1 Кинематика):

,

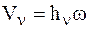где w – угловая скорость НМС, а h_n – расстояние от n-й точки НМС до оси z.

Момент количества движения n-й МТ относительно оси Oz примет вид:

.

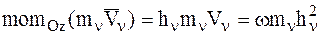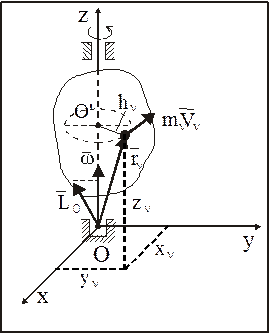
Рис. 33

Тогда кинетический момент НМС относительно неподвижной оси определится из соотношения:

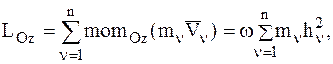
здесь 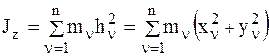– момент инерции НМС относительно оси Oz.

Итак, для кинетического момента НМС, вращающейся относительно неподвижной оси, получим:

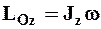. (4.28)

Величина кинетического момента НМС, вращающейся относительно неподвижной оси, равна произведению момента инерции НМС относительно той же оси на угловую скорость НМС (4.28).

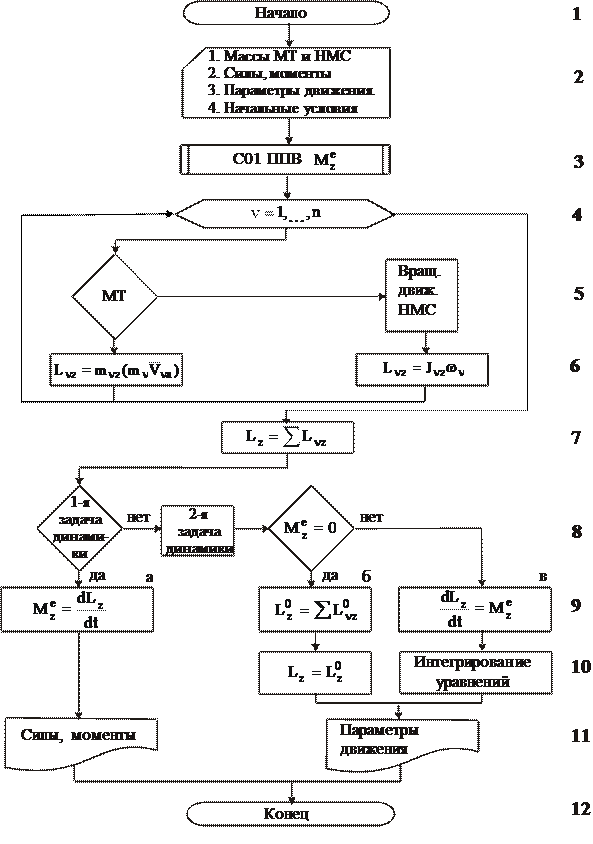
4.7. Алгоритм решения задач с помощью теоремы об изменении кинетического момента СМТ – схема алгоритма Д47 КМС с комментариями и примерами