Пространственная система сил

Пусть имеется произвольная пространственная система сил 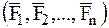. Используя основную теорему статики, перенесем все силы системы параллельно самим себе в произвольный центр О (рис. 25):

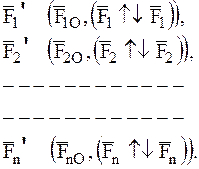
В результате получим:

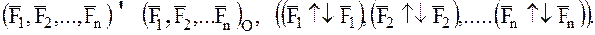
система сходящихся система пар

сил в точке О

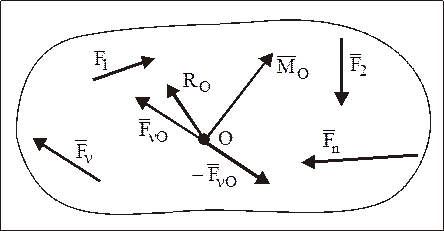
Рис. 25

Система сходящихся сил (глава 2) приводится к одной силе:

,

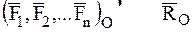где на основании соотношения (2.1) можно записать:

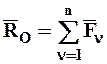. (4.3)

Система пар (глава 3) приводится к одной паре:

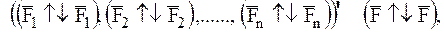
момент которой на основании соотношений (3.10), (4.2) и (1.2) определится формулой:

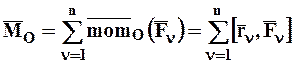. (4.4)

Итак,

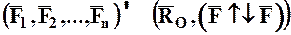(4.5)

или условно можно записать:

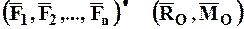. (4.6)

Таким образом, произвольная система сил всегда может быть приведена в произвольно выбранной точке – центре приведения к силе, равной геометрической сумме всех сил и называемой ее главным вектором, и к паре сил с моментом, равным геометрической сумме моментов всех сил системы относительно центра приведения и называемым ее главным моментом.