Трубопроводы с насосной подачей жидкости
Рассмотрим совместную работу трубопровода с насосом (такая система еще называется – трубопровод с насосной подачей). В общем случае это трубопровод, по которому насос перекачивает жидкость из нижнего резервуара с давлением на поверхности р0 в другой резервуар с давлением на поверхности рз, рис. 12.1
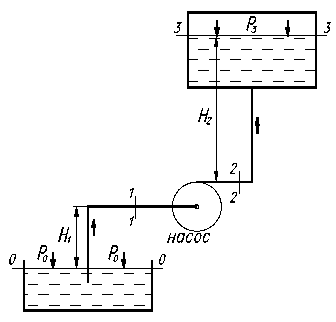 Рис.12.1. Рис.12.1.
| Высота расположения оси насоса относительно нижнего уровня Н1 называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом или всасывающей линией. Высота расположения конечного сечения трубопровода или верхнего уровня жидкости Н2 называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания. |
Составим уравнение Бернулли для потока во всасывающем трубопроводе, т. е. для сечений 0 – 0 и 1 – 1 (принимается α=1):
|
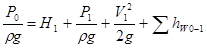
Это уравнение является основным для расчета всасывающих трубопроводов. Оно показывает, что процесс всасывания, т. е. подъем жидкости на высоту Н1, сообщение ей кинетической энергии и преодоление всех гидравлических сопротивлений происходит за счет использования (с помощью насоса) давления р0. Во время работы насоса на его входе создается вакуум и жидкость под действием разности давлений (атмосферного и низкого давления на входе) поступает в насос. Возможны следующие задачи расчета всасывающего трубопровода.
Задача 1. Даны все геометрические параметры трубопровода и расход.
Требуется найти абсолютное давление перед входом в насос.
Решение этой задачи представляет поверочный расчет всасывающего трубопровода. Абсолютное давление Р1, полученное по уравнению (12.1) сравнивают с тем, которое является минимально допустимым.
Задача 2. Дано минимально допустимое абсолютное давление перед входом в насос Р1.
Требуется найти одну из следующих предельных величин: H1min, Qmax, dmin, p0min. Эта задача также решается с помощью уравнения (12.1).
Для уравнения запишем уравнение Бернулли для напорного трубопровода, т. е. для сечений 2 – 2 и 3 – 3:
|
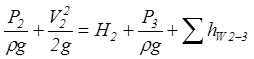
Левая часть уравнения (12.2) представляет энергию жидкости на выходе из насоса, отнесенную к единице веса. Энергия жидкости перед входом в насос может быть найдена из уравнения (12.1)
|
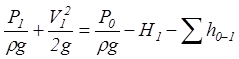
найдем приращение энергии жидкости в насосе, т. е. определим ту энергию, которую приобретает, проходя через насос каждая единица веса. Эта энергия сообщается жидкости насосом, поэтому она носит название напора, создаваемого насосом и обозначается обычно Ннас.
Для определения Ннас вычтем уравнение (12.3) из уравнения (12.2)
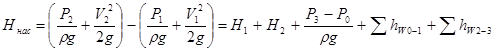
или
|
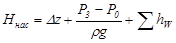
где Δz – полная геометрическая высота подъема жидкости, Σhw – сумма гидравлических потерь во всасывающем и напорном трубопроводах.
Если к действительной разности уровней Δz прибавить разность пьезометрических высот (p3 – p0)/ρg, то можно рассматривать как бы увеличенную разность уровней
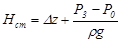
|
Ннас = Нст + Σhw
|
Ннас = Н.
Это равенство можно распространить на все случаи устойчивой работы насоса, соединенного с трубопроводом и сформулировать в виде правила: при установившемся течении в трубопроводе насос развивает напор, равный требуемому.
На равенстве (12.6) основывается метод расчета трубопроводов, питаемых насосом, который заключается в совместном построении, в одном масштабе и на одном графике двух кривых: напора H=f1(Q) по (12.5) – это фактически характеристика всех трубопроводов и характеристики насоса Hнас=f2(Q) и в нахождении точки их пересечения, рис. 12.2.
Дата добавления: 2015-08-01; просмотров: 1562;
