Характеристикой трубопровода называется график зависимости суммарных потерь напора в трубопроводе от расхода.
Для простого трубопровода потери равны требуемому напору, который в общем случае может быть найден по формуле
|
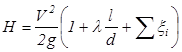 ,
,
которая при заданных значениях l, d, ∑ζi, Кэ однозначно отражает зависимость напора Н от расхода Q.
|
hW = H = KQ2 ,
а если учитывать только сопротивления по длине, то (11.2) примет вид
|
Зависимости (11.1) и (11.2) возможно представить в координатах H – Q, задавая ряд значений Q и определяя соответствующие им значения Н.
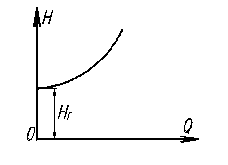
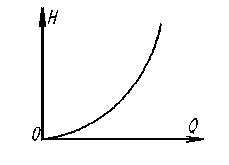


Полученная на рис. 11.1 кривая представляет геометрический образ характеристики трубопровода. Если помимо гидравлических сопротивлений необходимо еще преодолеть геометрический напор Нг (высоту Нг или эквивалентную разность давлений), то график (характеристика трубопровода) будет иметь вид как на рис. 11.2 (Н = Нг при Q=0).
 Пример. Рассмотрим расчет параллельного соединения простых трубопроводов в общем случае, когда заранее неизвестны зоны сопротивления в ветвях. Допустим, что имеются три ветви (число их на ход расчета не влияет).
Пример. Рассмотрим расчет параллельного соединения простых трубопроводов в общем случае, когда заранее неизвестны зоны сопротивления в ветвях. Допустим, что имеются три ветви (число их на ход расчета не влияет).
Заданы: общий расход и параметры каждой из ветвей. Необходимо найти потери напора и расход в каждой из них.
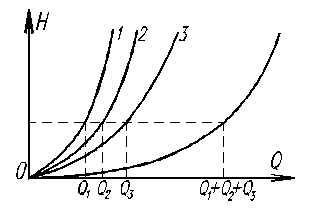
 Для решения задачи строим на одном графике в координатах H – Q характеристики всех ветвей, рис. 11.3 (в общем случае все они будут разные). Затем строим результирующую характеристику по нескольким точкам. Для этого при некотором значении Н, одинаковом для всех характеристик суммируем расходы и получаем точку для построения результирующей характеристики. После того, как она построена по нескольким точкам, откладываем на оси Q заданный суммарный (общий) расход, находим искомое значение Н и по каждой из характеристик ветвей находим значения расходов Q1, Q2 и Q3.
Для решения задачи строим на одном графике в координатах H – Q характеристики всех ветвей, рис. 11.3 (в общем случае все они будут разные). Затем строим результирующую характеристику по нескольким точкам. Для этого при некотором значении Н, одинаковом для всех характеристик суммируем расходы и получаем точку для построения результирующей характеристики. После того, как она построена по нескольким точкам, откладываем на оси Q заданный суммарный (общий) расход, находим искомое значение Н и по каждой из характеристик ветвей находим значения расходов Q1, Q2 и Q3.
Задача 11.1. Построить характеристику трубопровода, по которому при ламинарном режиме жидкость перетекает из одного резервуара в другой при постоянной разности уровней Н (принять, что местные потери отсутствуют и давление на свободной поверхности резервуаров атмосферное).
Указание Учесть выражение для λ при ламинарном режиме в формуле
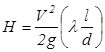 .
.
Дата добавления: 2015-08-01; просмотров: 2212;
