Принцип суперпозиции электростатических полей.

Основной задачей электростатики является определение величины и направ­ле­ния вектора напряженности 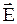в каждой точке поля, создаваемого либо системой неподвижных точечных зарядов, либо заряженными поверхностями произвольной формы. Рассмотрим первый случай, когда поле создано системой зарядов q₁, q₂,..., q_n. Если в какую-либо точку этого поля поместить пробный заряд q₀, то на него со стороны зарядов q₁, q₂,..., q_n будут действовать кулоновские силы 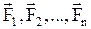. Со­гласно принципу независимости действия сил, рассмотренного в механике, равно­дей­ствующая сила 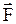равна их векторной сумме

.

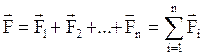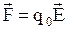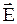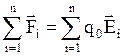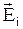Используя формулу напряженности электростатического поля, левую часть ра­венства можно записать: , где - напряженность результирующего поля, создаваемого всей системой зарядов в точке, где расположен пробный заряд q₀. Пра­вую часть равенства соответственно можно записать , где - напря­женность поля, создаваемая одним зарядом q_i. Равенство примет вид 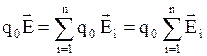. Сокращая на q₀, получим .

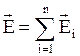Напряженность электростатического поля системы точечных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из этих зарядов в отдельности. В этом заключается принцип независимости действия электростатических полей или принцип суперпозиции (наложения) полей.

Обозначим через 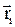радиус-вектор, проведенный из точечного заряда q_i в ис­следуемую точку поля. Напряженность поля в ней от заряда q_i равна 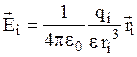. Тогда результирующая напряженность 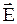, создаваемая всей системой зарядов равна 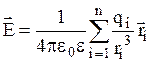. Полученная формула применима и для расчета электростатических полей за­ря­женных тел произвольной формы так как любое тело можно разделить на очень малые части, каж­дую из которых можно считать точечным зарядом q_i. Тогда расчет 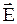в любой точке пространства будет аналогичен выше приведенному.