Корнями многочлена (1) называются решения уравнения

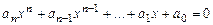. (2)

Например,

1) многочлен 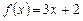имеет один действительный корень , т.к. уравнение 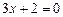имеет только одно решение ,

2) многочлен 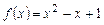имеет два комплексных корня 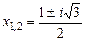, являющихся решениями квадратного уравнения .

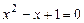Эти примеры показывают, что многочлен с действительными коэффициентами может иметь как действительные, так и комплексные корни.

Корень многочлена (1) является корнем кратности 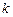, если он встречается 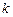раз среди всех корней уравнения (2). Например,

1) многочлен 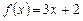имеет один корень . Это означает, что является однократным корнем (или корнем кратности 1).

2) , 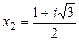- корни кратности 1 многочлена .

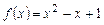3) многочлен 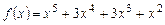можно переписать следующим образом:

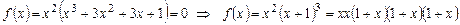. Следовательно, многочлен 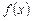имеет пять корней: 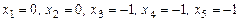. И значит,

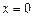- корень кратности 2, и 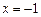- корень кратности 3 многочлена .

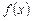Пример 1. Найти корни многочлена 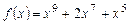и указать их кратность.

Решение.

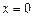- корень кратности 2, и 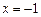- корень кратности 3 многочлена .

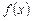- корень кратности 5, и 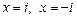- корни кратности 2 многочлена .

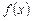Опять отметим, что многочлен с действительными коэффициентами из примера 1 наряду с действительным корнем 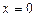имеет также комплексные корни .

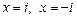Нахождение всех корней произвольно заданного многочлена часто бывает проблематичным. Если корни многочленов 1-го и 2-го порядка находятся достаточно просто, то поиск корней многочленов 3-го и 4-го порядка алгебраическими методами хотя и возможен, но уже не так прост: громоздкие аналитические выкладки (см., например, Г.Корн, Т.Корн. Справочник по математике, пункты: 1.8-3, … , 1.8.-6.) препятствуют широкому практическому применению аналитических методов нахождения корней этих многочленов. Для многочленов 5-го и более высокого порядков нахождение корней алгебраическими методами (т.е. с помощью конечного числа операций сложения, вычитания, умножения, деления, возведения в рациональную степень действительных чисел), в общем случае, невозможно. Поэтому, обычно корни многочленов выше 2-го порядка находят в приближенном виде вычислительными методами (эти методы изучаются в курсе математического анализа и численных методов). Далее рассматриваются примеры, в которых нахождение корней многочлена либо сводится к решению квадратных уравнений, либо не потребуется.

Деление многочлена на многочлен (алгоритм Евклида). Целая и дробная части отношения двух многочленов.

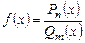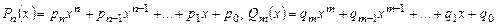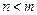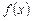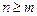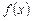Рассмотрим отношение двух многочленов , называемое дробно рациональной функцией: - многочлены степени соответственно. Если , то называется правильной дробно рациональной функцией (или проще, правильной дробью). Если же , то называется неправильной дробно рациональной функцией (или неправильной дробью). Для неправильной дроби справедлива следующая теорема.

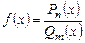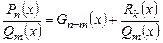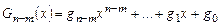Теорема. Неправильную дробь можно разложить в сумму многочлена и правильной дроби: , где - многочлен степен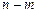и , и 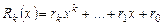- многочлен степени 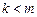. Такое разложение единственно. Многочлен 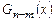называется целой частью, правильная дробь 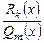- дробной частью, многочлен 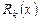- остатком от деления многочлена 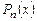на многочлен .

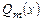Нахождение целой части и остатка от деления многочлена на многочлен производится по алгоритму Евклида. Приведем применение этого алгоритма на конкретных примерах.

Пример 2. Найти целую часть и остаток от деления многочлена 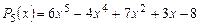на многочлен .

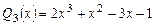Решение. 1-й шаг алгоритма Евклида.

Начало схемы алгоритма.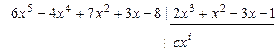

Подбираем постоянные 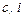так, чтобы при умножении 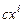на старший член 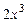делителя 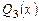получился старший член 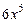многочлена 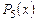. Очевидно, следует взять 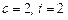. Подставляем 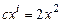и умножаем его на делитель 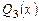. В результате получим многочлен 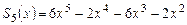. Записываем его слева под многочленом 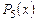. Находим разность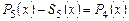 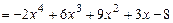и записываем этот многочлен слева под чертой под многочленом 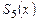. Степень многочлена 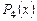больше степени делителя (многочлена 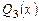), поэтому алгоритм Эвклида имеет продолжение.

2-й шаг. Записываем итоги вычислений 1-го шага. Прибавим слева к слагаемому 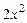новый член .

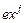Продолжение схемы алгоритма.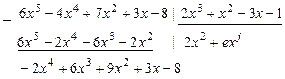

Константы 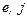подбираем так, чтобы при умножении 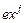на старший член 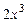делителя 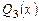получилось 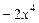. Очевидно, 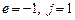. Подставляем 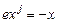и умножаем его на делитель 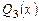, в результате получим многочлен 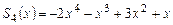. Записываем этот многочлен слева под многочленом 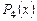. Находим разность 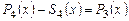, где 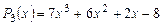и записываем этот многочлен слева под чертой под 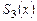. Степень многочлена 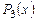равна степени делителя (многочлена 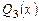), поэтому алгоритм Эвклида продолжается.

3-й шаг. Записываем итоги вычислений 2-го шага. Прибавим слева к слагаемым 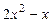новый член .

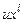Продолжение схемы алгоритма.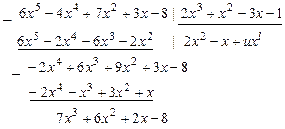

Константы 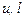подбираем так, чтобы при умножении 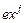на старший член 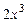делителя 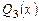было равно 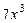. Очевидно, 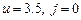. Подставляем 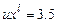и умножаем его на делитель 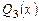, в результате получим многочлен 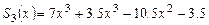. Записываем этот многочлен слева под 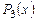. Находим разность 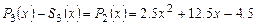и записываем ее слева под чертой под 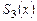. Степень многочлена 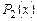меньше степени делителя 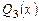, поэтому алгоритм Евклида закончился. Ответы таковы: целая часть и остаток от деления многочлена 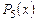на многочлен 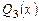соответственно равны 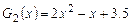и .

В окончательном виде схема алгоритма Евклида выглядит так.

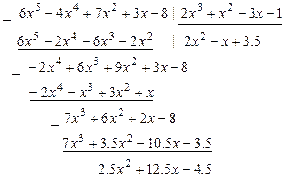
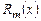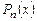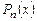Если остаток от деления многочлена на многочлен равен нулю, то многочлен нацело делится на многочлен . В этом случае многочлен называется делителем многочлена 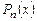, и многочлен 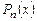можно записать в виде произведения .

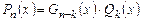Пример 3. Разложить в произведение многочлен 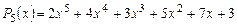, если известно, что многочлен 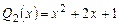нацело делит многочлен .

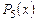Решение. С помощью алгоритма Евклида найдем целую часть 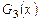от деления 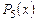на .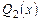

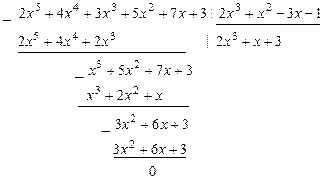
Следовательно, 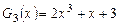и многочлен 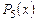можно разложить в произведение: .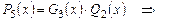

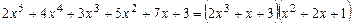2. Особую роль играет деление многочлена 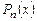на многочлен .

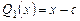Справедлива следующая теорема Безу. Остаток от деления многочлена 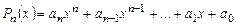на многочл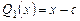ен равен .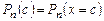

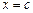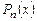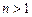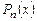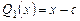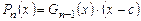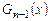Следствие теоремы Безу. Если - корень многочлена степени , то многочлен нацело делится на многочлен , т.е. , где - многочлен степени .

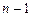Основная теорема алгебры многочленов: любой многочлен степени 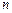имеет ровно 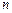корней, считая каждый корень столько раз, какова его кратность.

Согласно этой теореме любой многочлен 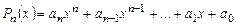с комплексными коэффициентами разлагается в следующее произведение

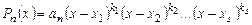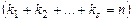, (1)

где 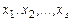- все корни многочлена 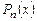, имеющие кратности 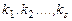соответственно. Такое разложение называется разложением многочлена 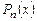над множеством комплексных чисел (над полем 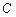). При разложении многочлена над полем 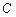автоматически считается, что 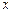может принимать любые комплексные значения.

Линейные многочлены 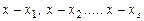являются неприводимыми многочленами над полем 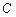. Многочлен называется неприводимым над заданным множеством чисел, если его нельзя разложить в произведение двух многочленов со степенями один и выше. Очевидно, что любой многочлен степени 1 неприводим над полем 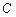, алюбой многочлен степени 2 и выше приводим над полем 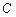, т.к. согласно основной теореме его можно разложить в произведение многочленов.

Пример 4. Разложить над полем 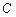многочлен .

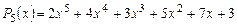Решение. Согласно примеру 3 заданный многочлен разлагается в произведение 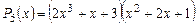. Первый множитель – многочлен 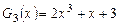имеет корень 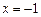, т.к. 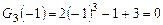. Следовательно, 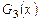нацело делится на многочлен 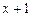. По алгоритму Евклида находим результат деления 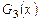на .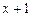

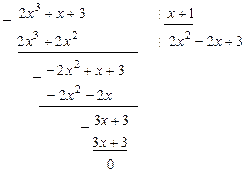
Значит, .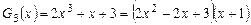

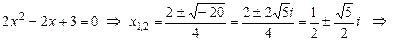
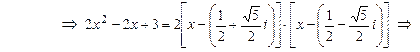
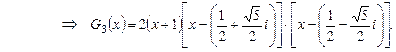
Поскольку, 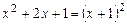, получим такое разложение многочлена над полем .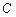

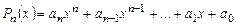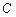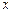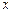Если многочлен имеет действительные коэффициенты, то наряду с его разложением над полем (когда считается комплексной величиной) возможно также разложение этого многочлена на множестве действительных чисел (над полем ), когда переменная принимает только действительные значения, и соответственно 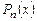принимает только действительные значения. При разложении многочлена с действительными коэффициентами над полем следует помнить, что не все многочлены второго порядка приводимы над полем .

Например, многочлен 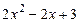приводим над полем 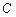, он допускает разложение 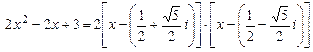и неприводим над полем , т.к. каждый из множителей в квадратных скобках принимает комплексные значения при действительных значениях переменной 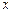. Поэтому, разложение многочлена 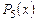из примера 4 над полем будет иметь следующий вид: 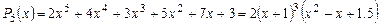. Здесь каждый из множителей принимает только действительные значения при действительных 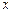. Чтобы получить это разложение, нужно перемножить квадратные скобки в найденном выше разложении многочлена 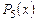над полем .

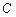Следует помнить также следующий факт: если многочлен с действительными коэффициентами имеет комплексный корень 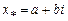, то комплексное сопряжение этого корня 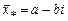также является корнем этого многочлена. Согласно этому факту и основной теореме алгебры многочленов разложение многочлена с действительными коэффициентами над полем в общем случае имеет следующий вид

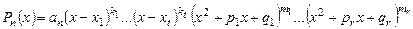, (2)

где 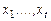- действительные корни кратности соответственно, а квадратные многочлены 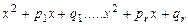имеют комплексно сопряженные корни.

Пример 5. Найти разложения многочлена 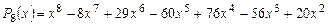на множестве комплексных (над полем 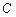) и на множестве действительных (над полем ) чисел, если известно, что 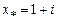- корень кратности 2 этого многочлена.

Решение.

1) 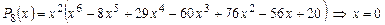- действительный корень кратности 2 многочлена .

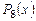2) 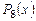- многочлен с действительными коэффициентами 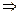вместе с комплексным корнем 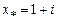кратности 2 этот многочлен имеет корень 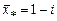тоже кратности 2 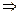в разложении многочлена 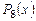над полем 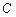(см. формулу (1)) будет присутствовать множитель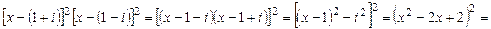

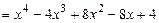
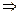многочлен 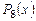, и значит, многочлен 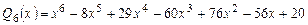нацело делится на многочлен .

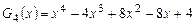3) Найдем результат деления 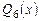на 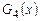по алгоритму Евклида.

.

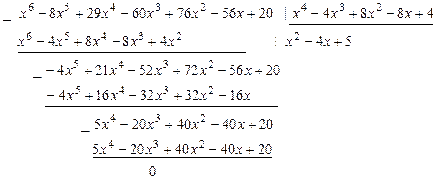
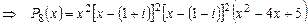4) Теперь найдем корни квадратного трехчлена .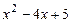

.

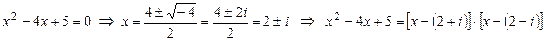Следовательно,разложение заданного многочлена 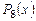над полем 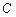имеет вид

.

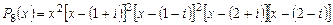Из этого разложения видно, что 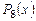имеет корни 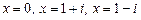кратности 2 и корни 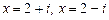кратности 1.

Чтобы найти разложение многочлена 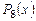над полем нужно перемножить скобки с сопряженными комплексными корнями. Т.к. 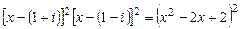и 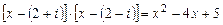, получаем следующее разложение многочлена 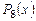над полем : .

_______________________________________________________________________

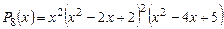Домашнее задание.

1. Найти все корни многочлена 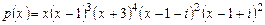и указать их кратность.

2. Найти целую и дробную части отношения 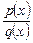, где , .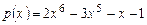

3. Найти разложения многочлена 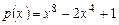на множестве комплексных и на множестве действительных чисел.