Извлечение корня -й степени из комплексного числа проводится по формуле Муавра-Лапласа
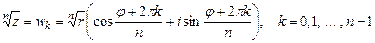 . (6)
. (6)
Из формулы (6) видно, что 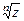 имеет ровно
имеет ровно 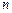 различных значений
различных значений 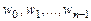 .
.
Пример 8. Найти все значения 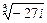 .
.
Решение. Требуется вычислить 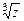 в случае
в случае 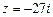 .
.
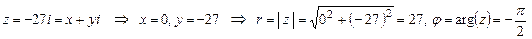 .
.
Формула Муавра-Лапласа (6), подставляя в которую 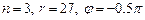 , дает:
, дает:
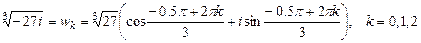 .
.
Следовательно,
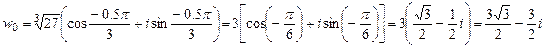 ,
,
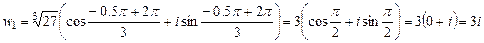 ,
,
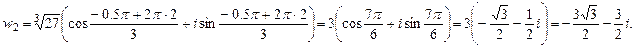 Итак,
Итак, 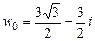 ,
, 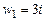 ,
, 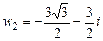 - искомые значения
- искомые значения 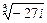 .
.
Пример 9. Найти в показательной форме все значения 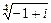 .
.
Решение. Требуется вычислить 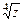 в случае
в случае 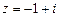 .
.
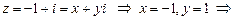
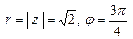 (см. число
(см. число 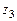 из примера 5).
из примера 5).
По формуле Муавра-Лапласа, в которой следует положить 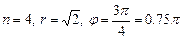 ,
,
для значений 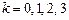 последовательно находим требуемые значения
последовательно находим требуемые значения 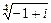 :
:
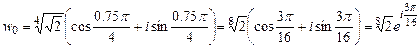 .
.
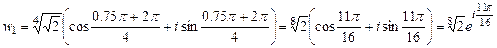 .
.
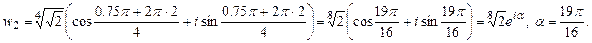
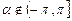 ,
, 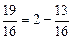 . Заменим
. Заменим 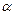 на
на 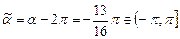 , получим окончательное выражение
, получим окончательное выражение 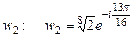 .
.
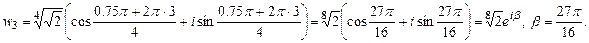
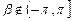 ,
, 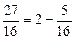 . Заменим
. Заменим 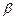 на
на 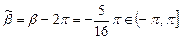 , получим окончательное выражение
, получим окончательное выражение 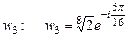 .
.
___________________________________________________________________
Домашнее задание.
1. Найти действительную и мнимую части, модуль и аргумент следующих комплексных чисел: 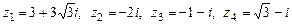 . Изобразить эти числа на комплексной плоскости. Представить эти числа в показательной и тригонометрической формах.
. Изобразить эти числа на комплексной плоскости. Представить эти числа в показательной и тригонометрической формах.
2. Найти 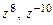 для комплексного числа
для комплексного числа 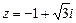 .
.
3. Найти все значения 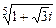 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Россия и ближнее зарубежье | | | Корнями многочлена (1) называются решения уравнения |
Дата добавления: 2015-07-30; просмотров: 1314;
