Способ №2

Уравнению 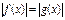соответствует равносильная совокупность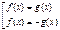

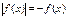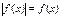IV) Уравнения вида и решаются следующим образом.

Уравнению 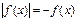соответствует равносильное неравенство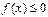

Уравнению 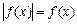соответствует равносильное неравенство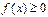

Методы решения иррациональных неравенств.

I) Неравенствах вида 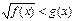решаются следующим образом.

Если 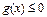, то решений нет.

Если 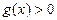, то неравенству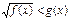

соответствует равносильная система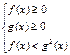

II) Неравенствах вида 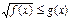решаются следующим образом.

Если 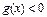, то решений нет.

Если , то неравенству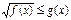

соответствует равносильная система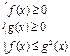

III) Неравенствах вида 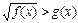решаются следующим образом.

Неравенству 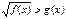соответствует равносильная совокупность систем.

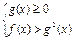или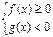

IV) Неравенствах вида 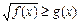решаются следующим образом.

Неравенству 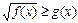соответствует равносильная совокупность систем.

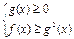или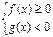

V) Неравенствах вида 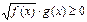решаются следующим образом.

Неравенству 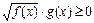соответствует равносильная совокупность систем.

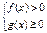или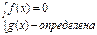

VI) Неравенствах вида 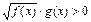решаются следующим образом.

Неравенству 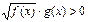соответствует равносильная система.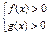

VII) Неравенствах вида 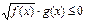решаются следующим образом.

Неравенству 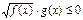соответствует равносильная совокупность систем.

или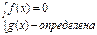

VIII) Неравенствах вида 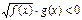решаются следующим образом.

Неравенству 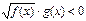соответствует равносильная система.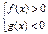

IX) Неравенствах вида 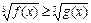решаются следующим образом.

Неравенству 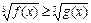соответствует равносильное неравенство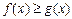

X) Неравенствах вида 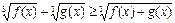решаются следующим образом.

Неравенству 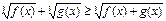соответствует равносильное неравенство.

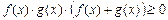
XI) Неравенствах вида 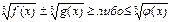решаются следующим образом.

Неравенство 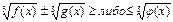решается обобщенным методом интервалов.

Методы решения иррациональных уравнений.