Основные классы моделей
Как отмечалось ранее, основой случайных процессов изменения ОП являются необратимые случайные изменения ОП, вызванные старением, износом или разрегулированием и имеющие определенную зависимость от времени. При этом случайный характер таких изменений обусловлен случайными параметрами, не зависящими от времени. Следовательно, модели реального изменения ОП объекта должны представлять случайные функции, аргументами которых являются постоянные во времени случайные величины и само время.
Рассмотрим наиболее распространенные модели (классы моделей) нестационарных случайных процессов приближения к отказам.
Линейные случайные функции
При линеаризации реального процесса износа объекта каждая реализация Хj (t) процесса заменяется прямой, т.е. реальный процесс изменения ОП Х(t) аппроксимируется случайной функцией вида
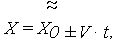
| (5) |
где Х0 = Х(t=0) = {x}0 - случайное начальное значение ОП (при t = 0), имеющее математическое ожидание (МО) mxo = M{Х0} и среднее квадратичное отклонение (СКО) Sxo =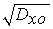 
; V{v} - случайная нормально распределенная скорость изменения ОП во времени, обладающая МО mv = M{V} и CКО S v = 
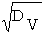. Нелинейные случайные функции
Для многих объектов типична некоторая постоянная относительная скорость изменения ОП
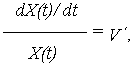
что соответствует нелинейному случайному процессу Х(t), аппроксимируемому случайной функцией вида
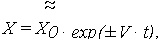
| (6) |
где Х0 = Х(t=0) = {x}0 - как и ранее, случайное начальное значение ОП; V' - случайная, нормально распределенная скорость изменения натурального логарифма ОП во времени, имеющая МО mv = M{V } и СКО Sv =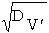 
.
В моделях обоих классов (5) и (6) знаки "+" и "-" используются для аппроксимации соответственно возрастающих и убывающих во времени процессов. Cлучайная величина Х0 в моделях (5), (6) является постоянной во времени, как и случайная величина скорости V изменения ОП в модели (5). В модели (6) постоянной во времени является скорость изменения логарифма ОП, сам же ОП имеет переменную во времени скорость изменения.
В дальнейшем для простоты обозначения будем полагать, что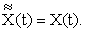 
Для удобства дальнейшего рассмотрения моделей только в линейном варианте модель (6) путем логарифмирования преобразуем к линейной модели изменения логарифма ОП:
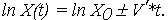
| (7) |
Обозначая натуральный логарифм ОП случайной функцией Y(t)
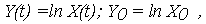
| (8) |
выражение (7) можно представить в виде
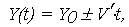
| (9) |
подобном модели (5).
Рассмотрим раздельно каждый тип линейных случайных моделей, аппроксимирующих случайный процесс изменения ОП Х(t) или его логарифма Y(t).
14.3.2. Основные типы моделей
Из различных модификаций линейных возрастающих случайных функций изменения ОП Х(t) или ln X(t) наиболее часто процесс приближения объекта к отказам аппроксимируется следующими типами моделей:
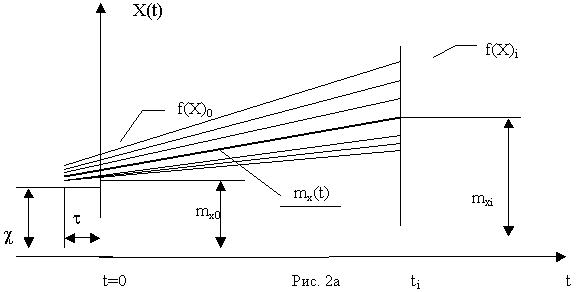
а) веерной с ненулевым начальным рассеиванием (рис. 2a);
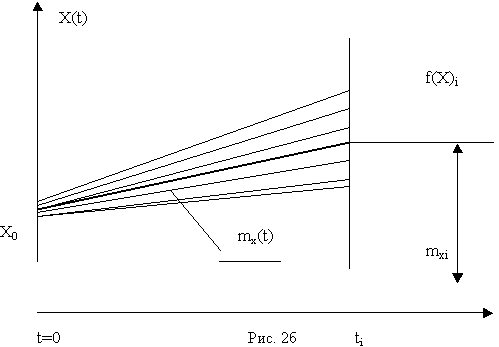
б) веерной с нулевым начальным рассеиванием (рис. 2б);
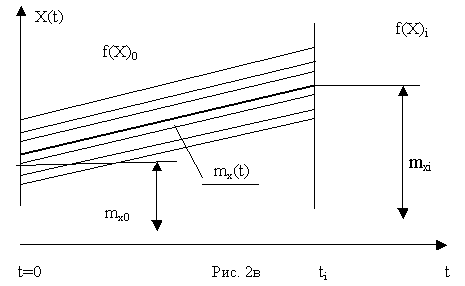
в) равномерной (рис. 2в).
| ||
| ||
|
Тип модели линейной функции Х(t) или ln X(t) зависит от числа случайных аргументов, определяющих ее случайный характер.
Веерная функция с ненулевым начальным рассеиванием описывается:
- для процесса X(t)
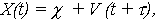
| (10) |
- для процесса ln X(t)
| (11) |
При t = 0 значения функций (12) и (13) представляют собой случайную величину, соответственно
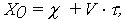
| (12) |
и
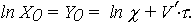
| (13) |
причем V = V' . С учетом (12) и (13) модели (10), (11) легко представляются в виде (5) и (9). Случайный характер рассмотренной модели определяется двумя случайными аргументами: X0 или ln X0 - случайное начальное значение ОП или его логарифма; V или V' - случайная скорость изменения ОП или его логарифма.
Как следует из рис. 2a, все реализации веерной линейной случайной функции с ненулевым начальным рассеиванием проходят через общую неслучайную точку - "полюс".
Аргумент рассмотренной модели - случайная скорость изменения ОП (V) или логарифма ОП (V ) - имеет нормальное распределение с плотностью распределения соответственно:
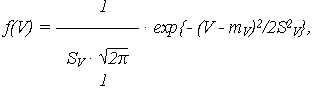
| (14) |
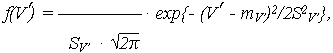
| (15) |
Линейно зависящая от V случайная функция Х(t) (10) во всех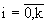 
сечениях будет распределена нормально с плотностью
и параметрами распределения:
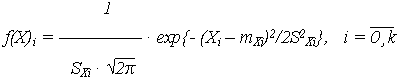
| (16) |
- матожидание mXi = M{Xi};
- среднее квадратичное отклонение
- Численные характеристики - матожидание mx(t) и СКО Sx(t), самой случайной функции (10) выражаются через числовые характеристики mv и Sv случайной скорости:
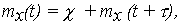
| (17) | |
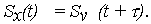
| (18) | |
Cлучайное начальное значение ОП X0 соответствует сечению функции Х(t) (10) при t =0, поэтому также имеет нормальное распределение по (16) при i = 0 с параметрами mx(t = 0) = mx0 и СКО Sx(t = 0) = Sx0 , определяемыми из (17) и (18) при t=0:
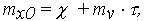
| (19) | |
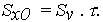
| (20) | |
С учетом (19) и (20) выражения (17), (18) для числовых характеристик случайной функции (10) изменения ОП Х(t) примут вид:
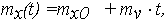
| (21) |
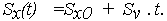
| (22) |
В соответствие с (11) нормальное распределение скорости V' приводит к тому, что линейно зависящий от V' логарифм ОП ln X(t) = Y(t) также будет распределен нормально во всех 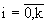- сечениях с плотностью распределения
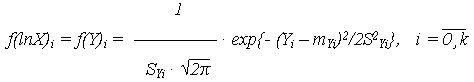
| (23) |
Cам же ОП при этом будет иметь логарифмически нормальное распределение, плотность которого:
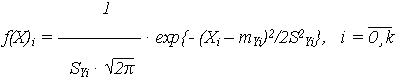
| (24) |
В выражениях (23), (24)
myi = M{lnXi},
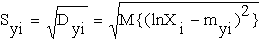- соответственно, матожидание и СКО логарифма ОП в 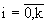сечениях случайной функции (11).
Матожидание my(t) и СКО Sy(t) линеаризованной путем логарифмирования функции (11) можно получить, используя числовые характеристики случайной скорости V : mv' и Sv'. Проводя аналогичные, как для функции (10), преобразования, получаем числовые характеристики модели (11) изменения логарифма ОП lnX(t) = Y(t):
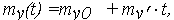
| (25) |
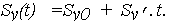
| (26) |
Веерная функция с нулевым начальным рассеиванием является частным случаем модели (5), (9) и может быть получена из указанных выражений путем замены в них, соответственно, случайных начальных значений ОП Х0 или его логарифма lnX0 = Y0 некоторым неслучайным значением K0 или lnK0.
Поскольку веерная модель с ненулевым начальным рассеиванием является
частным случаем моделей (10), (11), то ее свойства определяются свойствами указанных моделей, поэтому числовые характеристики определяются (без вывода):
- для функции Х(t) = K0 + Vt изменения ОП из (21), (22)
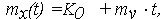
| (27) | |
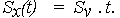
| (28) | |
- для функции Y(t) = lnX(t) = lnK0 + V't изменения ОП из (25), (26)
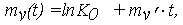
| (29) |
| (30) |
Равномерная функция также является частным случаем моделей (5), (9) и может быть получена из последних путем замены в них соответственно случайных скоростей изменения ОП V или его логарифма V' на неслучайные (постоянные) скорости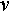 
или '.
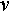Числовые характеристики случайных функций определяются (без вывода):
- для функции изменения ОП Х(t) = X0 + 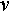t из (21), (22)
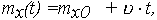
| (31) |
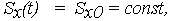
| (32) |
- для функции Y(t) = lnX(t) = Y0 + 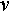't из (25), (26)
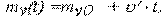
| (33) | |
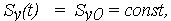
| (34) | |
Рассмотренные линейные модели удобны для аппроксимации случайных процессов изменения ОП тем, что позволяют характеризовать эти процессы ограниченным числом аргументов модели, для определения которых требуется минимальный объем экспериментальных данных.
Контрольные вопросы:
10. Поясните смысл и природу постепенных отказов?
11. Что называется определяющим параметром, и в чем заключается условие работоспособности объекта?
12. Что представляет собой время сохранения работоспособности?
13. Из каких составляющих состоит случайный процесс изменения определяющего параметра? Дайте характеристику каждой составляющей?
14. Как изменяется определяющий параметр в зависимости от наработки объекта?
15. Перечислите основные классы моделей приближения объекта к отказам, в чем их принципиальное отличие?
16. Перечислите основные типы моделей приближения объекта к отказам, в чем их принципиальное отличие?
Дата добавления: 2015-07-30; просмотров: 981;