СИСТЕМЫ ПОРОЖДЕНИЯ. ОСНОВНЫЕ ПОНЯТИЯ
Процессы обработки упорядоченной системы данных D порождают новые системы данных, которые в совокупности с исходными данными будем называть системами порождения F [1]:
D ® {f} ® F; (D = D1) ® (F = D2); D1 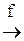 D2;
D2;
где D - система данных (D Û D1):
D = (I, d); I = (V, W); d: W ® V; I Û D0;
F - система порождения; F Û D2;
{f}- операции порождения.
Операции порождения определяются формальными, логическими и эвристическими правилами преобразования системы D в систему F в цепочке: I ® D ® F или D0 ® D1 ® D2.
Если процесс порождения D в F не меняет исходной базы системы D и при этом сохраняется изоморфизм отношений систем D и F, то такие операции порождения классифицируются как операции структуризации или просто структуризация (C).
В противном случае имеем метаоперацию (М).
Очевидно, что операции "С" и "М" могут применяться многократно и в любой последовательности : СF, МF; СМF; С2F...
Пример
В табл. П.2.1 имеется пять столбцов данных. Первые три столбца определяют систему данных D. Четвертый и пятый столбцы построены по функции порождения вида:
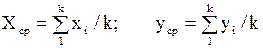 (6.9)
(6.9)
Порождаемая система данных F - это 4-й и 5-й столбцы таблицы.
Для рациональной системы порождения, представляющей множество уравнений связи между D и F, можно построить вычислительную модель и спроектировать вычислительный процесс формирования системы F, удобный для реализации перехода от D к F. Этот процесс, как правило, имитирует действия оператора в пошаговом режиме обработки данных. Например, при вычислении средних значений процесс порождения строить по формуле:
 (6.10)
(6.10)
В этом случае в таблицу D ® F вводится дополнительный столбец для 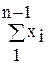 .
.
Вычислительный процесс строится по рекурсивной цепочке как показано ни рис.6.2.
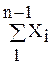
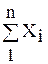 Xср(n)
Xср(n)
(n =: n +1)
Подобные процессы удобно описывать на основе понятий маски и системы адресных уравнений [1,58]. На рис. 6.2 приведена маска и система адресных уравнений для примера данных, приведенных в приложении П1.
На рис. 6.2 комплекс D Þ {f} Þ F представлен на уровне алгебраического описания как М: N1 * N2 Þ N3, N1 = {0;...12}; N2 = {0,…4}. Значения N3 определяются системой данных и правилами порождения {f}. Множества N1 и N2 определяют адреса строк и столбцов соответственно. Множество пар N1 * N2 определяет систему координат ячеек таблицы. Так как процессы рекурсивные, подобные формуле (6.10), то порождение новых данных (F) удобно описывать не в абсолютной системе координат, а в одной из относительных систем координат: обычно относительно достигнутого состояния вычислительного процесса.
Рассмотрим пооперационно преобразования, на основе которых можно строить системные технологии обработки данных, применять современные средства (типа электронных таблиц) для реализации подобных процессов.
Дата добавления: 2015-07-30; просмотров: 811;
