Переход от автомата Мили к автомату Мура и обратно
Абстрактный автомат может работать, как некоторый преобразователь входного слова в слова выходного алфавита
Пусть на вход этого автомата поступает входное слово –  (последовательность входных сигналов).
(последовательность входных сигналов).
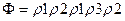
Назовем переменную 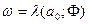 реакцией автомата, находящегося в состоянии а0, на входное слово
реакцией автомата, находящегося в состоянии а0, на входное слово  .
.
Автомат Мили в ответ на входное слово длиной k выдает последовательность состояний длиной k+1 и выходное слово длиной k.
Зададим автомат Мура.
Найдем реакцию автомата Мура на входное слово –  . Начальное состояние x1:
. Начальное состояние x1:
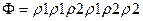
x1x4x2x1x4x3x5
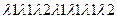
Два автомата SА и SB с одинаковыми входным и выходным алфавитом называются - эквивалентными, если после установления их в начальное состояние реакции на любое входное слово совпадают.
Можно показать, что для любого автомата Мили существует эквивалентный ему автомат Мура, и наоборот. При написании алгоритма взаимной трансформации часто пренебрегают выходным сигналом, связанным с начальным состоянием.
Рассмотрим переход от автомата Мура к автомату Мили.
Пусть задан автомат Мура:
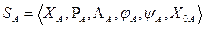
Необходимо построить автомат Мили, эквивалентный автомату Мура:

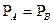

Функцию  определим следующим образом: если в автомате Мура имеются функции
определим следующим образом: если в автомате Мура имеются функции 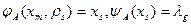 , то для автомата Мили можно записать следующую функцию выхода:
, то для автомата Мили можно записать следующую функцию выхода: 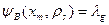 .
.
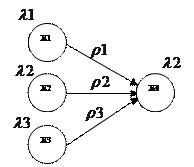
Рассмотрим переход от автомата Мура к автомату Мили с помощью графа:
Для осуществления перехода от автомата Мура к автомату Мили выходной сигнал 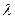 , находящийся в автомате Мура рядом с вершиной, для автомата Мили передается на все дуги, входящие в эту вершину.
, находящийся в автомате Мура рядом с вершиной, для автомата Мили передается на все дуги, входящие в эту вершину.
 | |||
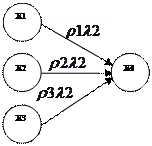 |
Переход от автомата Мура к Мили табличным способом:
Поскольку таблица переходов автомата Мура полностью совпадает с таблицей переходов автомата Мили, то основная проблема при описании автомата Мили табличным способом – это составление таблицы выходов. Таблица выходов автомата Мили получается из таблицы переходов автомата Мура путем замены символа соответствующего внутреннему состоянию автомата Мура символом выходного сигнала.
Для автомата Мура
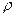 1 1
| 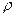 2 2
| 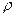 3 3
| ||
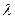 1 1
| X1 | X1 | X2 | X4 |
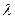 2 2
| X2 | X2 | X3 | X1 |
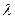 1 1
| X3 | X1 | X3 | X4 |
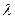 3 3
| X4 | X1 | X1 | X4 |
Для автомата Мили
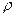 1 1
| 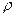 2 2
| 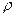 3 3
| |
| X1 | 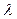 1 1
| 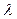 2 2
| 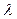 3 3
|
| X2 | 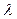 2 2
| 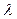 1 1
| 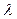 1 1
|
| X3 | 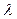 1 1
| 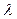 1 1
| 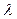 3 3
|
| X4 | 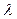 1 1
| 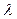 1 1
| 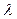 3 3
|
Из самого способа построения автомата Мили очевидно, что он эквивалентен автомату Мура.
Для входной последовательности Ф поведение автоматов Sа и полностью совпадают. По индукции не трудно доказать, что любое входное слово конечной длины, поданное на входы автоматов Sа и SВ, установленных в начальное состояние x0 вызовет появление одинаковых выходных слов.
Переход от автомата Мили к автомату Мура. При переходе от автомата Мили к автомату Мура необходимо наложить следующие ограничения: в автомате Мили не должно быть преходящих состояний.
Преходящее состояние - это состояние, в которое при представлении автомата в виде графа не входит ни одна дуга и которое имеет хотя бы одну выходящую дугу.
Задан автомат Мили Sа . Необходимо построить автомат Мура SВ.
Алфавиты должны совпадать:
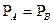
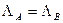
Для определения множества XB каждому состоянию  поставим соответствующее множество пар вида
поставим соответствующее множество пар вида  ,где
,где  -это выходной сигнал приписанный дуге, входящей в xs.
-это выходной сигнал приписанный дуге, входящей в xs.
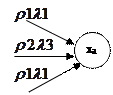 |

Число элементов в множестве XS будет равно числу различных выходных сигналов на дугах автомата Мили SA, входящих в состояние xa Число внутренних состояний автомата Мура будет определяться объединением множеств всех XS.
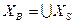
XA => XB
Функция переходов 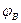 и функция выходов
и функция выходов 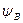 определяется так: если в автомате Мили имеется переход из состояния xm в состояние xs под воздействием
определяется так: если в автомате Мили имеется переход из состояния xm в состояние xs под воздействием 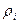
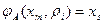
и при этом выдается выходной сигнал 
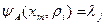 ,
,
то в автомате Мура будет переход из множества состояний X’m, порождаемое внутренним состоянием xm под воздействием входного сигнала 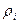 .
.
 .
.
Функция выходов автомата Мура определяется следующим образом
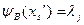
В качестве начального состояния x0B можно взять любое состояние из множества, которое порождается начальным состоянием x0А.
 Т.о. получается автомат SВ, эквивалентный автомату SA.
Т.о. получается автомат SВ, эквивалентный автомату SA.
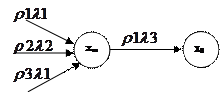 |
Автомат Мили Автомат Мура
Изложенные методы взаимных транспозиций модели Мили и Мура показывают, что при переходе от автомата Мура к Мили число состояний автомата не меняется, а при обратном переходе число состояний, как правило, возрастает.
Вследствие транзитивности отношения эквивалентности 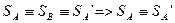 . Два автомата Мили также будут эквивалентны, хотя у последнего на два состояния больше. Таким образом, эквивалентные автоматы могут иметь различное число внутренних состояний. В связи с этим возникла задача нахождения минимального автомата в классе эквивалентных между собой автоматов.
. Два автомата Мили также будут эквивалентны, хотя у последнего на два состояния больше. Таким образом, эквивалентные автоматы могут иметь различное число внутренних состояний. В связи с этим возникла задача нахождения минимального автомата в классе эквивалентных между собой автоматов.
Дата добавления: 2015-07-30; просмотров: 4446;
