Разделимые коды с обнаружением ошибок
Из названного класса рассмотрим принципы образования и характеристики следующих кодов: код с проверкой паритета (на четность или нечетность); код с простым повторением, инверсный код; корреляционный код.
Правила образования этих кодов ясны из приводимой ниже таблицы.
| N0 | Примитивный безизбыточный код | Код с проверкой на нечетность | Код с простым повторением | Инверсный код | Корреляционный код |
| 000 1 | 000 000 | 000 000 | 01 01 01 | ||
| 001 0 | 001 001 | 001 110 | 01 01 10 | ||
| 010 0 | 010 010 | 010 101 | 01 10 01 | ||
| 011 1 | 011 011 | 011 011 | 01 10 10 | ||
| 100 0 | 100 100 | 100 011 | 10 01 01 | ||
| 101 1 | 101 101 | 101 101 | 10 01 10 | ||
| 110 1 | 110 110 | 110 110 | 10 10 01 | ||
| 111 0 | 111 111 | 111 000 | 10 10 10 |
1. При приеме кода с проверкой на нечетность содержимое всех разрядов кодовой комбинации суммируется по модулю два. Если результат этой операции равен 1 (что будет при нечетном числе единиц в кодовой комбинации), то полагается , что комбинация принята правильно. Если результат операции равен 0, что будет при четном числе единиц в кодовой комбинации, то полагается, что комбинация принята с ошибкой и выполняется защитный отказ.
Этот код обнаруживает все ошибки нечетной кратности. Мощность кода Np = 2n-1. Коэффициент избыточности 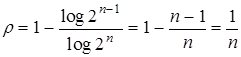 , т.е. уменьшается с увеличением числа разрядов кодовой комбинации.
, т.е. уменьшается с увеличением числа разрядов кодовой комбинации.
Для разделимых равномерных двоичных кодов формулу для коэффициента избыточности можно упростить :
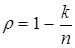 ,
,
где n - общее число разрядов в кодовой комбинации, k- число информационных разрядов в кодовой комбинации.
2. При приеме кода с простым повторением осуществляется сравнение k информационных разрядов комбинации с остальными n-k контрольными разрядами. Если значения сравниваемых одноименных разрядов совпадают, то комбинация полагается принятой верно. В противном случае реализуется защитный отказ. Этот код обнаруживает все ошибки нечетной кратности и часть ошибок четной кратности. Мощность кода Np = 2n/2. Коэффициент избыточности 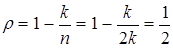 .
.
3. Прием инверсного кода осуществляется в два этапа. На первом этапе анализируется четность информационной части комбинации. Если она четна, то проверочная часть остается без изменения. Если она нечетна, то проверочная часть инвертируется. На втором этапе информационная часть поразрядно сравнивается с проверочной. Если они совпадают, то полагается, что комбинация принята верно. Этот код обнаруживает все ошибки кратностью 1,2,5,6 и большую часть 3- и 4-кратных ошибок. Мощность кода и коэффициент избыточности имеют те же значения, что и для кода с простым повторением.
4. При приеме корреляционного кода сравниваются парные элементы кодовой комбинации. Если хотя бы в одном случае они совпадают, принимается решение об ошибочно принятой комбинации. Характеристики кода полностью совпадают с характеристиками кода с простым повторением.
Контрольные вопросы к лекции 9
9-1. Что называется кодированием в широком смысле?
9-2. Что называется алфавитом источника?
9-3. Что называется объемом алфавита источника?
9-4. Что называется кодированием в узком смысле?
9-5. Что называется кодовой комбинацией?
9-6. Что называется кодом?
9-7. Что называется основанием кода?
9-8. Какой код называется равномерным?
9-9. чем продиктована необходимость замены каждого символа источника совокупностью кодовых символов?
9-10. Какие комбинации кода называются разрешенными?
9-11. Что называется мощностью кода?
9-12. Что является численной характеристикой избыточности кода?
9-13. Какой код называется безизбыточным?
9-14. Почему безизбыточные коды не обладают помехоустойчивостью?
9-15. Какое кодирование называется помехоустойчивым?
9-16. Какие коды называются кодами с обнаружением ошибок?
9-17. Какие коды называются кодами с обнаружением ошибок?
9-18. Что называется кодовым расстоянием между двумя кодовыми комбинациями?
9-19. Какую операцию необходимо выполнить для определения кодового расстояния между двумя кодовыми комбинациями?
9-20. Что называется кодовым расстоянием кода?
9-21. Что называется вектором ошибки?
9-22. Что называется кратностью ошибки?
9-23. Перечислите параметры биномиального закона распределения кратности ошибок?
9-24. Как связаны кодовое расстояние кода и вероятность ошибочного декодирования?
9-25. Как связаны кодовое расстояние кода и кратность обнаруживаемых им ошибок?
9-26. Как связаны кодовое расстояние кода и кратность исправляемых им ошибок?
9-27. Какой избыточный код называется блоковым?
9-28. Какой избыточный код называется разделимым?
9-29. Какой разделимый избыточный код называется систематическим?
9-30. Почему большинство систематических разделимых кодов называются линейными?
9-31. Что называется спектром кода?
9-32. Что является характерной особенностью кодов, называемых циклическими?
9-33. Чему равна мощность кода на одно сочетание?
9-34. Как осуществляется декодирование кода на одно сочетание?
9-35. Является ли код на одно сочетание разделимым?
9-36. Как осуществляется декодирование кода с проверкой паритета?
9-37. Как определяется коэффициент избыточности для разделимых равномерных двоичных кодов?
9-38. Как осуществляется декодирование кода с простым повторением?
9-39. Как осуществляется декодирование инверсного кода?
9-40. Как осуществляется декодирование корреляционного кода?
Лекция 10. Коды с обобщенными проверками на четность
К групповым кодам с обнаружением и исправлением ошибок относятся коды с обобщенными проверками на четность и полиномиальные коды.
Все систематические коды являются разделимыми. Их принято иногда называть (n,k)-кодами, где n – общее число разрядов в кодовой комбинации, k- число информационных разрядов. Число контрольных разрядов в кодовой комбинации, следовательно, равно n-k.
Точных аналитических выражений, связывающих корректирующие свойства кода с его параметрами, не существует. Получены лишь асимптотические выражения, называемые границами, для кодового расстояния.
Наиболее важными и полезными границами для кодового расстояния являются граница Хэмминга, граница Плоткина и граница Варшамова – Гилберта.
Граница Хэмминга, выражаемая обычно следующим образом,
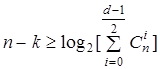 , ,
| (3.8) |
указывает на наибольшее число кодовых комбинаций, возможных при данных n и числе обнаруживаемых и исправляемых ошибок.
Граница Плоткина также является верхней границей для кодового расстояния при данных n и k и может выражаться следующим образом

| (3.9) |
Выражение (3.9) удобно для получения максимально возможного d при заданных n и k, но не очень удобно для получения максимального k при данных d и n, в связи с чем другая форма границы Плоткина выглядит следующим образом
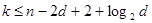
| (3.10) |
Граница Хэмминга обычно близка к оптимальной для высокоскоростных кодов (т.е. для больших значений k/n), а граница Плоткина – для низкоскоростных кодов.
Согласно границе Варшамова – Гилберта, выражаемой как
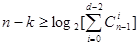
| (3.11) |
существует (n,k)-код с кодовым расстоянием, не меньшим d , и с числом проверок на четность, не превышающим n-k. Таким образом, граница Варшамова – Гилберта является границей существования и дает нижнюю оценку для кодового расстояния «наилучшего» кода.
Приведем пример использования этих границ. Предположим, что требуется найти код длиной n=63 с кодовым расстоянием d=5 и наибольшим возможным значением k. Примером такого кода является (63,51)-код БЧХ. Для оценки того, насколько хорошим является этот код, используем границы Хэмминга и Варшамова – Гилберта. Из (3.8) следует, что 2017 £ 2n-k , откуда n-k ³11.
Граница Варшамова – Гилберта (3.11) «утверждает», что 39774>2n-k, откуда n-k £16. Таким образом, из границы Хэмминга следует, что не существует кодов, обеспечивающих заданные параметры, с n-k<11, а граница Варшамова – Гилберта гарантирует существование таких кодов с n-k£16. Отсюда можно сделать вывод, что код (63,51) является «хорошим» и дальнейшие поиски могут привести лишь к незначительному улучшению.
Для кодов с d=3 для определения требуемого числа контрольных разрядов можно найти более простое выражение, воспользовавшись следующими рассуждениями. При передаче кодовой комбинации может быть искажен любой из n разрядов комбинации или комбинация принята без искажений. Следовательно, всего может быть n+1 вариантов исхода. Использование контрольных разрядов должно обеспечить возможность различения всех n+1 вариантов. С помощью n-k разрядов можно описать 2n-k событий, следовательно, должно выполняться условие 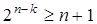 или
или
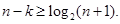
| (3.12) |
Рассматриваемые (n,k)-коды называются групповыми. Своим названием они обязаны тому, что множество кодовых комбинаций вместе с нулевой кодовой комбинацией, снабженное операцией посимвольного сложения по модулю два, образуют математическую структуру, называемую группой. Основные свойства группы:
1) замкнутость – т.е. сумма по модулю два двух элементов группы всегда лежит в группе,
2) ассоциативность – т.е. (aÅb)Åc=aÅ(bÅc),
3) наличие единичного элемента – для двоичных кодов это нулевая комбинация,
4) каждый элемент группы обладает обратным, для которого а+(-а)=0, для двоичных кодов каждая кодовая комбинация совпадает со своей обратной.
Каждая кодовая комбинация группового кода разбивается на две части. Первая часть содержит k информационных символов и всегда совпадает с передаваемой информационной последовательностью. Каждый из n-k символов второй части вычисляется как линейная комбинация фиксированного подмножества информационных символов. Согласно определениям, данным ранее, эти коды можно назвать также систематическими и линейными. Символы второй части, представляющие собой контрольные разряды, называются символами обобщенных проверок на четность.
Значения контрольных разрядов в каждой кодовой комбинации определяются в результате сложения по модулю два тех или иных информационных разрядов этой комбинации. Особенностью группового кода является постоянство набора информационных разрядов, определяющего данный контрольный разряд. Другими словами, для данного группового кода имеется единый алгоритм образования значений контрольных разрядов по значениям информационных разрядов, определяемый т.н. проверочными уравнениями.
Пусть кодовая комбинация двоичного группового кода имеет n разрядов: unun-1un-2 . . . u1. Положим, что среди этих n разрядов символы ur, ul, us - контрольные. Число проверочных уравнений определяется числом контрольных символов:

| (3.13) |
В этих уравнениях коэффициенты 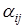 принимают значения 1 или 0 в зависимости от того, используется или нет соответственно для определения значения i-го контрольного разряда j-й информационный разряд.
принимают значения 1 или 0 в зависимости от того, используется или нет соответственно для определения значения i-го контрольного разряда j-й информационный разряд.
С помощью этих уравнений могут быть составлены все Np=2k разрешенных или рабочих комбинаций кода путем записи информационных разрядов каждой комбинации и вычисления значений контрольных разрядов по уравнениям (3.13) для каждой комбинации информационных разрядов. Таким образом, тот или иной код может быть задан таблицей информационных кодовых комбинаций и системой проверочных уравнений.
Однако свойство линейности групповых кодов обеспечивает возможность более компактной записи кода. Из свойств групповых кодов вытекает, что все множество кодовых комбинаций данного кода можно получить путем суммирования по модулю два в различных сочетаниях т.н. образующих кодовых комбинаций или базисных векторов.
Удобно в качестве образующих выбрать комбинации, которые содержать лишь по одной единице в информационных разрядах. Следовательно, число таких комбинаций равно k – числу информационных разрядов. Если к тому же упорядочить разряды, расположив слева направо сначала информационные разряды, начиная со старшего, а затем контрольные разряды, и записать упорядоченные таким образом комбинации одна под другой, то получим матрицу, содержащую n столбцов и k строк, которая называется образующей матрицей систематического (n,k)-кода и обозначается Gn,k.
Пример.3.2. Построить образующую матрицу (7,4)-кода, имеющего следующие проверочные уравнения
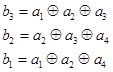
Решение. Сначала целесообразно построить полную таблицу кода в соответствии с проверочными уравнениями.
| a4 | a3 | a2 | a1 | b3 | b2 | b1 |
Выберем образующие кодовые комбинации (выделены жирным шрифтом) и запишем их в виде образующей матрицы.
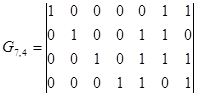 .
.
При наличии образующей матрицы можно найти все остальные кодовые комбинации кода без использования полной таблицы кода. Например, требуется найти кодовую комбинацию для информационной комбинации 1101. Для этого нужно суммировать по модулю два три соответствующих строки образующей матрицы:
Å 0100110
0001101
1101000,
после чего можно сопоставить результат с полной таблицей кода.
Анализ вида образующей матрицы приводит к выводу, что она состоит из двух матриц – единичной
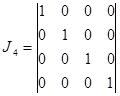 и дополняющей
и дополняющей 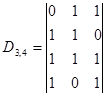 .
.
Обобщая рассмотренный пример на любой систематический групповой блоковый (n,k)-код можно записать для него образующую матрицу
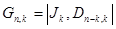
| (3.14) |
Единичная матрица является образующей для равномерного примитивного кода, поскольку с ее помощью могут быть построены все 2k-1 ненулевых комбинаций этого кода путем суммирования по модулю два ее строк в различных сочетаниях.
Дополняющая матрица, если не заданы проверочные уравнения, может быть получена путем подбора k различных комбинаций, содержащих n-k разрядов. Эти комбинации должны удовлетворять следующим условиям :
1) количество единиц в комбинации должно быть не менее d-1,
2) сумма по модулю два любых двух комбинаций должна содержать не менее d-2 единиц.
Пример.3.3. Построить образующую матрицу систематического кода (7,4) с d=3.
Решение. Начать построение целесообразно с нахождения дополняющей матрицы 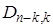 в данном случае n=7, k=4, n-k=3, т.е.D3,4. Следовательно, надо подобрать трехразрядные комбинации, каждая из которых содержит по d-1=3-1=2 единицы. Поскольку таких комбинаций всего три, а их требуется k=4, то в качестве четвертой выберем, не нарушая первого условия, комбинацию, содержащую три единицы. Тогда дополняющая матрица
в данном случае n=7, k=4, n-k=3, т.е.D3,4. Следовательно, надо подобрать трехразрядные комбинации, каждая из которых содержит по d-1=3-1=2 единицы. Поскольку таких комбинаций всего три, а их требуется k=4, то в качестве четвертой выберем, не нарушая первого условия, комбинацию, содержащую три единицы. Тогда дополняющая матрица
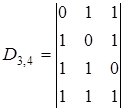
и образующая матрица
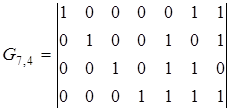
| (3.15) |
из которой может быть найдена система проверочных уравнений
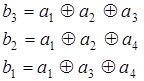
| (3.16) |
Сравнивая примеры 3.2 и 3.3 можно сделать вывод: для каждой образующей матрицы Gn,k существует своя единственная система проверочных уравнений и, наоборот, поскольку то и другое является описанием одного и того же кода.
В качестве еще одной равноправной формы описания систематического (n,k)-кода служит т.н. проверочная матрица, обозначаемая обычно Hn,n-k. При построении проверочной матрицы к единичной квадратной матрице Jn-k слева приписывают матрицу, содержащую k столбцов и n-k строк, причем каждая ее строка формируется из соответствующего столбца дополняющей матрицы, т.е. приписываемая матрица представляет собой транспонированную дополняющую матрицу
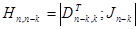
| (3.17) |
Пример.3.4. Для кода из примера 3.3- построить проверочную матрицу.
Решение
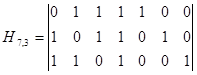
| (3.18) |
Проверочная матрица позволяет выбрать алгоритм кодирования и декодирования, исходя из того, что единицы в каждой ее строке соответствуют тем символам кодовой комбинации, сумма которых по модулю два должна быть равна 0. Так, из матрицы (3.18) можно получить следующие уравнения проверок:
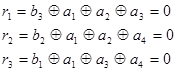
| (3.19) |
Естественно, что (3.16) и (3.19) полностью совпадают с той лишь разницей, что операции по (3.16) выполняются при кодировании для получения значений контрольных разрядов в каждой кодовой комбинации, а операции по (3.19) выполняются при декодировании для обнаружения и исправления ошибок.
Из анализа (3.19) видно, что a1 входит во все три уравнения, а2 - в первое и второе, а3 – в первое и третье, а4 – во второе и третье. Следовательно, искажение любого аi нарушит вполне определенные уравнения, т.е. сумма по модулю два в них будет равна не нулю, а единице. По тому, какие именно уравнения нарушены, можно определить, в каком разряде произошла ошибка, и восстановить его истинное значение.
Таким образом, результаты проверок дают кодовую комбинацию вида 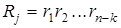 , которую называют контрольной последовательностью или, чаще, синдромом.
, которую называют контрольной последовательностью или, чаще, синдромом.
При 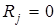 считается, что кодовая комбинация принята верно или произошла не обнаруживаемая ошибка. Если
считается, что кодовая комбинация принята верно или произошла не обнаруживаемая ошибка. Если 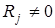 , считается, что комбинация принята неверно, т.е. имеет место обнаружение ошибки. Если (n,k)-код используется только для обнаружения ошибок, то в теории кодирования доказывается, что при любой вероятности ошибочного приема кодового символа р £ 1/2 найдется код, для которого вероятность необнаруженной ошибки будет меньше вполне определенного значения
, считается, что комбинация принята неверно, т.е. имеет место обнаружение ошибки. Если (n,k)-код используется только для обнаружения ошибок, то в теории кодирования доказывается, что при любой вероятности ошибочного приема кодового символа р £ 1/2 найдется код, для которого вероятность необнаруженной ошибки будет меньше вполне определенного значения 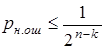 . Такие коды называются кодами равномерно обнаруживающими ошибки.
. Такие коды называются кодами равномерно обнаруживающими ошибки.
Для исправления ошибок каждому ненулевому синдрому может быть сопоставлен исправляющий вектор Ej , сумма по модулю два которого с принятой кодовой комбинацией образует переданную комбинацию. Пусть, например, передается кодовая комбинация из примера 3.3
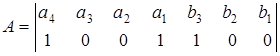 ,
,
а принимается
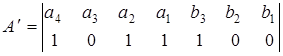 .
.
При выполнении проверок на приеме в соответствии с системой (3.19) получается
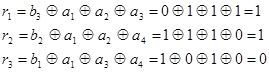 ,
,
т.е. синдром R=110, нарушены 1 и 2 уравнения, в которые входит а2, следовательно, ошибка в разряде а2 и тогда исправляющий вектор Е=0010000, а исправленная кодовая комбинация
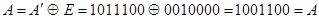 .
.
Пользуясь этим примером, обратим внимание на третью стоку образующей матрицы (3.15). В части этой строки, соответствующей единичной матрице, единица расположена на месте разряда, в котором произошла ошибка, а получившийся синдром R равен части этой же строки, входящей в дополняющую матрицу.
Обобщая, можно сказать, что при ошибке в разряде а4 синдром будет 011, при ошибке в разряде а3 – 101, при ошибке в разряде а1 – 111.
То же самое следует из проверочной матрицы этого кода (3.18), где первый столбец – синдром при ошибке в разряде а4 и т.д.
На основании любого из приведенных ранее описаний группового систематического кода (системы проверочных уравнений, образующей матрицы, проверочной матрицы) могут быть синтезированы функциональные схемы кодера и декодера такого кода.
Дата добавления: 2015-07-30; просмотров: 2011;
