Передаточная функция (1 стр 1)

Если на вход любой системы подать сигнал синусоидальной формы:

x_вх(t) = X_m cos(wt) = X_m e ^jwt .

Очевидно, что выходной сигнал будет иметь ту же форму:

x_вых(t) = Y_m cos(wt+j) = Y_m e ^j(wt+j) .

Зависимость же между амплитудами и фазами выходного и входного сигналов определяет ДУ движения системы. Возмем произвольное, считая помеху f(t) равной нулю:

(T₂² p² + T₁ p + 1) x_вых(t) = (k₁ + k₂ p) x_вх(t) .

Подставим сигналы в уравнение движения:

T₂²(jw)² X_вых e ^j(wt+j) + T₁(jw) X_вых e ^j(wt+j) + X_вых e ^j(wt+j) = k₁ X_вх e ^jwt + k₂(jw) X_вх e ^jwt .

Найдем отношение выходного сигнала ко входному:

.

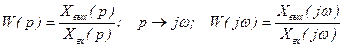Вывод 1: Частотная передаточная функция получается из обычной заменой оператора Лапласа s на комплексную частоту jw, т.е. в результате перехода от изображения Лапласа к изображению Фурье.

Вывод 2: ДУ движения системы связывает входной и выходной сигналы (т.е. функции времени), ПФ связывет изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры.

Частотная передаточная функция может быть представлена в следующих видах:

W(jw) = A(w) e ^jj(w), или W(jw) = P(w) + jQ(w) ;

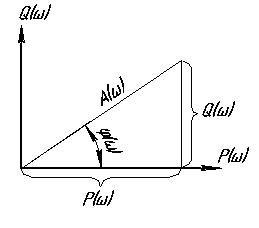где: W(jw) – амплитудно-фазовая частотная характеристика (АФЧХ);

• A(w) - модуль частотной передаточной функции - находится как отношение модулей числителя и знаменателя (АЧХ):
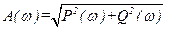
• j(w) - фаза частотной передаточной функции - находится как разность аргументов числителя и знаменателя (ФЧХ):
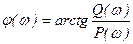
• P(w) и Q(w) - вещественная и мнимая части частотной ПФ. Для их нахождения необходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину. Логарифмические ЧХ - ЛАЧХ & ЛФЧХПостроение ЛАЧХ & ЛФЧХ производится по выражениям: L(w) = lg |W(jw)| = lg A(w), [лог]; j(w) = arg(W(jw)), [рад].