Уравнение состояния системы

В настоящем разделе изучается одноконтурная аналоговая динамическая система автоматического управления. Динамической называется любая физическая система, все элементы которой, и в первую очередь объект управления, описываются с помощью обыкновенных дифференциальных уравнений.

Для математического описания динамики рассматриваемой системы используется метод пространства состояний. Вводится n-мерный вектор состояния системы

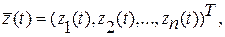(2.1)

«T» - знак транспонирования.

Составляющие вектора (2.1) называются переменными состояния.

Система управляемая, поэтому вводится r-мерный вектор управления

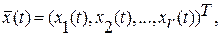(2.2)

т.е. система обладает r степенями свободы и управления.

Динамика описывается системой n дифференциальных уравнений состояния, решенных относительно производных переменных состояния первого порядка

. (2.3)

Векторное уравнение состояния системы имеет вид

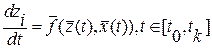, (2.4)

где 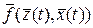- непрерывно дифференцируемая по всем своим аргументам вектор-функция (в рассматриваемом случае стационарная).

Переменные состояния 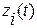есть функции времени, в результате чего вектор состояния в пространстве состояния описывает кривую, называемую траекторией движения системы.

Выходные (измеряемые или наблюдаемые) величины образуют n-мерный вектор 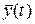, связанный с векторами состояния и управления зависимостью

(2.5)

где 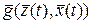- дифференцируемая n-мерная вектор-функция.

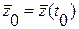При заданных векторах управления и начальных условий интегрирование уравнения состояния (2.4) позволяет определить зависимость и в соответствии с уравнением (2.5) – закон изменения входной величины , т.е. динамический режим работы системы.