КММ уровня непараметрической статики

Второй уровень представления КММ включает в рассмотрение отображение 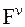, определяющее правила преобразования входов 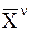в выходы 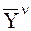, т.е. что необходимо сделать, чтобы при условии 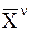получить 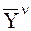, адекватное целевому функционированию элемента 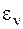. В общем случае 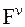— отображение может быть представлено скалярной или векторной функцией, а также функционалом или оператором. Концептуальная метамодель уровня непараметрической статики, следовательно, представляется кортежем вида

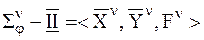. (14)

Раскрытие структуры преобразования вида 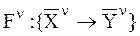является основной задачей КММ уровня 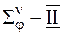. Рассмотрим в качестве иллюстрации функциональное описание элемента 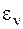, представленное скалярной функцией , причем: .

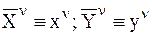Функционирование элемента 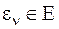( 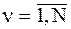) на УНС описывается как отображение 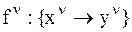. Это отображение называется функцией, если оно однозначно. Условия однозначности определяются следующим образом. Пусть заданы пары значений сигналов “вход — выход”:

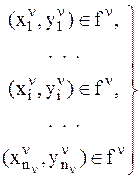. (15)

Если из условия ( 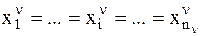), следует, что ( 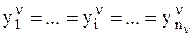), то отображение 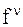однозначно. Значение величины 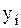в любой из пар 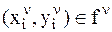называется функцией от данного 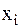. Общий вид записи функции 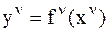позволяет дать формальное определение функции элемента 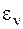в скалярной форме представления

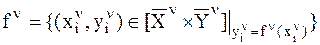. (16)

Таким образом, КММ (14) проинтерпретирована в КММ того же уровня, но в скалярной форме функционального представления. Отметим, что богатство концептуальных метамоделей 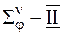функционирования системного элемента 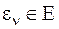( 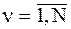) на уровне непараметрической статики определяется многообразием ее интерпретаций на математическом, логическом или логико-математическом языках описания (пред­став­ления) 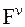-отображения.