Разложение несимметричной системы трёх векторов на системы прямой, обратной и нулевой последовательности чередования фаз
Любую несимметричную систему трёх токов, напряжений одинаковой частоты – обозначим их А́, В́, С́ – можно однозначно представить в виде трёх систем: прямой, обратной и нулевой последовательностей чередования фаз.
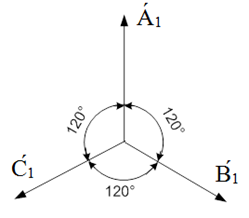
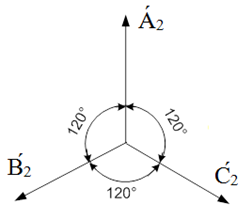
а) б) в)
Рис. 44. Системы прямой, обратной и нулевой последовательностей чередования фаз
Система прямой последовательности (рис. 44, а) состоит из трёх векторов А́1, В́1, С́1, равных по величине и повёрнутых относительно друг друга на 120°, причём вектор В́1 отстаёт от вектора А́1 на 120°, а вектор С́1 опережает А́1 на 120°. Используя оператор а трёхфазной системы, можно записать:
В́1 = а2 А́1; С́1 = а А́1; (133)
Система обратной последовательности (рис. 44, б) состоит из трёх векторов А́2, В́2, С́2, равных по величине и повёрнутых относительно друг друга на 120°, причём вектор В́2 опережает вектор А́2 на 120°, а вектор С́2 отстаёт от А́2 на 120°. Используя оператор а трёхфазной системы, можно записать:
В́2 = а2 А́2; С́2 = а А́2; (134)
Система нулевой последовательности (рис. 44, в) образована тремя одинаковыми векторами А́0, В́0, С́0, совпадающих по фазе.
А́0 = В́0 = С́0 (135)
Выразим заданные три вектора А́, В́, С́ через векторы симметричных систем следующим образом:
А́ = А́0 + А́1 + А́2
В́ = В́0 + В́1 + В́2 (136)
С́ = С́0 + С́1 + С́2
Перепишем (136) с учётом (133) и (134): 
А́ = А́0 + А́1 + А́2
В́ = В́0 + В́1 + В́2 а а2 (137)
С́ = С́0 + С́1 + С́2 а2 а
Сложим уравнения (137), учитывая, что 1 + а + а2 = 0. Получим
А́0 =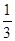 
( А́ + В́ + С́) (138)
Для определения А́1 надо второе уравнение в (137) умножить на а, а третье – на а2, и сложить все три уравнения:
А́1= 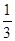( А́ + аВ́ + а2С́) (139)
Для определения А́2 надо второе уравнение в (137) умножить на а2, а третье – на а, и сложить все три уравнения:
А́2= 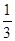( А́ + а2В́ + аС́) (140)
Дата добавления: 2015-07-30; просмотров: 1005;