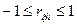Свойства. Если случайные величины ξ и h независимые, то они некоррелированные ( )

1. Если случайные величины ξ и h независимые, то они некоррелированные ( )

Если случайные величины ξ и h коррелированные ( 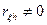), то эти случайные величины зависимы

Обратные утверждения неверны !

1. Нормированной случайной величиной называется отношение отклонения случайной величины от ее математического ожидания к стандартному отклонению

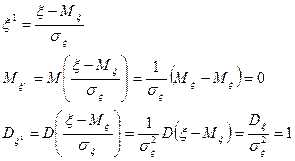
Коэффициент корреляции двух случайных величин ξ и h равен корреляционному моменту их нормированных случайных величин

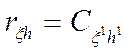
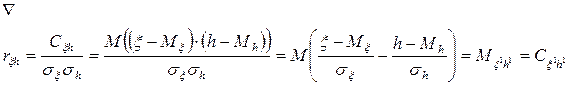
1. Если случайные величины ξ и h линейно-зависимые, то модуль коэффициента корреляции

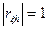
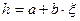где a,b произвольные коэффициенты.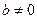

1.

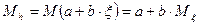
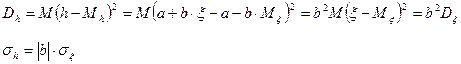
2.

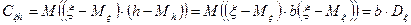
3.

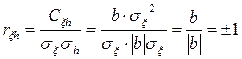
Если линейная зависимость между ξ и h носит возрастающий характер, тогда коэффициент корреляции равен 1. Если линейная зависимость между ξ и h носит убывающмй характер, тогда коэффициент корреляции равен -1.

1. Коэффициент корреляции является мерой линейной зависимости двух случайных величин

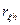
1. Степень линейной зависимости

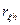
	0 ÷ 0.3	0.4 ÷ 0.7	0.8 ÷ 1
С.Л.З.	Слабая	Средняя	Сильная