ОПРЕДЕЛЕНИЕ ЭЛЕКТРОЕМКОСТИ КОНДЕНСАТОРА

Если уединенному проводнику сообщить электрический заряд 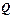, то потенциал проводника примет некоторое значение 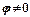, причем 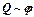, т.е. 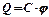. Следовательно,

-

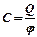электрическая емкость уединенного проводника. Единица ёмкости – фарад (Ф).

Конденсатором называется система из двух близко расположенных проводников (обкладок), разделенных слоем диэлектрика. В зависимости от формы обкладок конденсаторы бывают плоские, цилиндрические и сферические.

Под емкостью 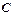конденсатора понимается физическая величина, равная отношению заряда 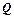, накопленного в конденсаторе, к разности потенциалов ( 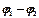) между его обкладками:

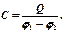
Электроемкость конденсатора зависит от его формы, геометрических размеров и диэлектрической проницаемости среды, заполняющей пространство между обкладками. В случае плоского конденсатора

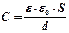, (1)

где 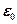=8,85·10^–12 Ф/м – электрическая постоянная; 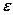– диэлектрическая проницаемость среды, заполняющей пространство между обкладками; 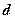– расстояние между пластинами, 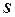- площадь обкладок.

Другой важнейшей характеристикой конденсатора является напряжение пробоя, т.е. минимальная разность потенциалов на обкладках, при которой происходит электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы и размеров обкладок и от свойств диэлектрика.

При практическом использовании конденсаторов для получения необходимой емкости собирают батареи из отдельных элементов, соединяя их последовательно или параллельно.

При последовательном соединении конденсаторов заряд на обкладках остается величиной постоянной: 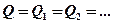, напряжения суммируются: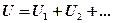

Тогда электроемкость:

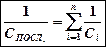. (2)

При последовательном соединении на каждый из конденсаторов приходится лишь часть разности потенциалов Δφ напряжения источника, вследствие чего уменьшается возможность пробоя конденсаторов.

При параллельном соединении конденсаторов напряжение остается величиной постоянной: 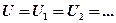, заряд батареи конденсаторов: .

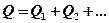Тогда общая электроемкость:

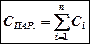. (3)

Пробивное напряжение такой батареи равно пробивному напряжению того из конденсаторов, у которого оно наименьшее.