Стоячие волны
Исследование собственных колебаний струны методом резонанса
Две когерентные и одинаковые по интенсивности волны, распространяющиеся навстречу друг другу, при определенных условиях могут создавать особого вида интерференционную картину, получившую название стоячих волн.
Интерференция – сложение в пространстве двух (или нескольких)волн, при котором в разных точках пространства происходит усиление или ослабление амплитуды результирующей волны. Интерференция возможна только для когерентных волн.
Когерентность – согласованное во времени и пространстве протекание колебательных или волновых процессов.
Стоячая волна представляет собой периодическое колебание с характерным пространственным распределением амплитуды – чередованием пучностей (максимумов амплитуды)и узлов (нулей амплитуды). Такая картина может возникать всякий раз, когда волна падает на хорошо отражающую преграду. Когерентность обеспечивается тем, что обе волны представляют собой раннюю и позднюю части одной и той же волны. Стоячие волны могут устанавливаться только при отсутствии затухания в среде и при полном отражении от границ.
Найдем уравнение стоячей волны, а также координаты ее узлов и пучностей. Пусть стоячая волна возникла при наложении двух встречных бегущих волн с одинаковыми скоростями 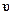 , циклическими частотами
, циклическими частотами 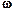 и амплитудам
и амплитудам 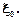 Уравнения волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, имеют вид:
Уравнения волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, имеют вид:
|
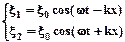
здесь 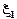 и
и 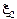 - смещения точки среды с координатой х в момент времени t, вызванные соответственно падающей и встречной волной.
- смещения точки среды с координатой х в момент времени t, вызванные соответственно падающей и встречной волной.
Сложив уравнения и учитывая, что волновое число k связано с длиной волны 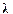 :
: 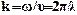 , получим уравнение стоячей волны:
, получим уравнение стоячей волны:
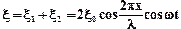 . (1)
. (1)
Из (1) видно, что в каждой точке стоячей волны происходят колебания с той же частотой 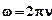 , что и у встречных волн,
, что и у встречных волн,
но с амплитудой 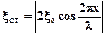 , зависящей от координаты х рассматриваемой точки.
, зависящей от координаты х рассматриваемой точки.
В пучностяхамплитуда стоячей волны максимальна и равна сумме амплитуд складываемых колебаний 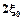 , поэтому координаты пучностей определим из условия:
, поэтому координаты пучностей определим из условия:
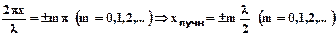 . (2)
. (2)
В узлах амплитуда стоячей волны равна нулю, и координаты узлов определим из условия:
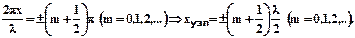 (3)
(3)
То есть в стоячей волне некоторые точки среды (пучности) колеблются с максимальной амплитудой, а некоторые точки (узлы) остаются неподвижными в течение всего колебательного процесса; остальные точки среды совершают колебания с некоторыми промежуточными амплитудами.
Можно видеть, что расстояние между соседними пучностями, как и расстояние между соседними узлами, равно 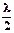 . Расстояние между соседними пучностью и узлом равно
. Расстояние между соседними пучностью и узлом равно 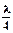 (рис.1).
(рис.1).
Множитель 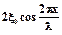 в уравнении стоячей волны при переходе через узел меняет знак, поэтому между двумя соседними узлами все точки среды колеблются синфазно, при переходе же через узел фаза изменяется на
в уравнении стоячей волны при переходе через узел меняет знак, поэтому между двумя соседними узлами все точки среды колеблются синфазно, при переходе же через узел фаза изменяется на 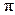 , то есть колебания по разные стороны от узла (в пределах полуволны) происходят в противофазе (рис.1).
, то есть колебания по разные стороны от узла (в пределах полуволны) происходят в противофазе (рис.1).
Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникает пучность (рис.1,а), если более плотная – узел (рис.1,б).
Отражаясь от более плотной среды, волна меняет свою фазу на противоположную и результат сложения этих колебаний дает узел (пример: в месте закрепления колеблющейся веревки получается узел). Этот факт принято называть «потерей полуволны».
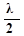
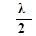
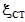

Рис. 1. График стоячей волны. На рисунке: 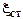 – амплитуда стоячей волны,
– амплитуда стоячей волны, 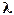 - длина волны, х – направление распространения.
- длина волны, х – направление распространения.
Отражаясь от менее плотной среды, волна не меняет фазы в месте отражения, поэтому потери полуволны не происходит; фазы падающей и отраженной волн одинаковы. В этом случае в результате сложения колебаний одинаковых фаз получается пучность (пример: свободный конец колеблющейся веревки образует пучность).
Как известно, бегущая волна в направлении ее движения переносит энергию колебательного движения. Стоячая волна энергию не переносит, поскольку падающая и отраженная волны, имея одинаковые амплитуды, несут одинаковую энергию, но в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узловыми точками, с течением времени остается неизменной. Только в пределах расстояний, равных половине длины волны, происходят взаимные превращения кинетической энергии в потенциальную и наоборот.
Колебания струны
В натянутой струне, закрепленной с обоих концов, при возбуждении произвольного поперечного возмущения может возникать стоячая волна. При этом на закрепленных концах струны должны выполняться определенные граничные условия: концы струны должны быть узлами стоячей волны. Это означает, что на длине струны 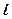 укладывается целое число
укладывается целое число 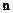 полуволн (рис. 2). Отсюда вытекает условие:
полуволн (рис. 2). Отсюда вытекает условие:
|
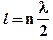 или
или 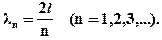
Этим длинам волн соответствуют частоты
|
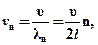
где 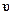 - фазовая скорость распространения бегущей волны в струне, которая может быть вычислена как
- фазовая скорость распространения бегущей волны в струне, которая может быть вычислена как
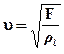 . (6)
. (6)
Здесь 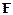 - сила натяжения струны;
- сила натяжения струны; 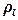 - линейная плотность струны, то есть масса единицы длины струны, вычисляется через
- линейная плотность струны, то есть масса единицы длины струны, вычисляется через
объемную плотность струны 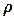 по формуле:
по формуле: 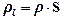 ;
;
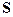 - площадь поперечного сечения струны. Таким образом, фазовая скорость бегущей волны вычисляется по формуле
- площадь поперечного сечения струны. Таким образом, фазовая скорость бегущей волны вычисляется по формуле
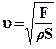 (7)
(7)
и выражение для частоты стоячей волны приобретает вид
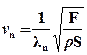 . (8)
. (8)
Частоты 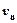 называются собственными частотами струны,
называются собственными частотами струны,
а соответствующие им гармонические колебания – собственными колебаниями, или гармониками. Частота 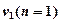 называется основной частотой, а остальные частоты
называется основной частотой, а остальные частоты 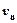 – обертонами.
– обертонами.
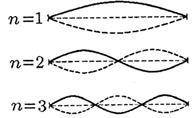
Рис. 2. Распределение амплитуд отдельных точек струны при собственных колебаниях струны для различных значений 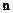 .
.
В общем случае колебания струны представляют собой суперпозицию (наложение) различных гармоник. В струне можно возбудить колебания, соответствующие одной из собственных частот.
В этом случае мы будем иметь условие резонанса струны.
Приборы и принадлежности: вертикальная стойка со струной, электромагнитный вибратор, источник напряжения, разновесы.
В работе исследуются колебания натянутой медной струны (гибкой однородной нити). Схема экспериментальной установки представлена на рис. 3. Внешнее периодическое воздействие на струну 1 осуществляется в верхней ее точке, где конец струны прикреплен к якорю электромагнитного вибратора 2. Электромагнитный вибратор питается от сети переменным током частотой 50 Гц. К нижнему концу струны прикреплена чашка весов 4,
а сама струна пропущена через отверстие малого диаметра в пластинке 3, которая может перемещаться вверх-вниз вдоль стойки.
Если нагрузить чашку весов гирьками и включить в сеть электромагнитный вибратор, то якорь электромагнита начнет совершать колебания с частотой тока сети, и по струне будут распространяться поперечные волны, которые, отражаясь от пластинки 3, образуют встречные волны. При наложении прямой и обратной волны образуются стоячие волны, если выполняется условие:
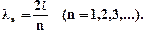
Подбирая длину струны и степень ее натяжения, можно наблюдать образование стоячей волны в струне. Длину струны с установившейся стоячей волной изменяют перемещением вверх-вниз пластинки 3. Силу натяжения F струны изменяют, меняя гирьки в чашке весов 4 (рис. 3).
 |
Рис. 3. Схема экспериментальной установки: 1 – струна, 2 – электро-магнитный вибратор, 3 – отражающая пластина, 4 - чашка весов.
Как видно из рисунка 3, в данной работе сила натяжения струны равна силе тяжести, действующей на чашку весов с грузом.
То есть в формуле (8) 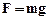 , где
, где 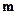 - масса чашки грузом;
- масса чашки грузом; 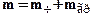 ,
, 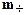 - масса чашки,
- масса чашки, 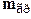 - масса груза.
- масса груза.
Таким образом, окончательно расчетная формула для частоты стоячей волны приобретает вид
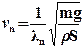 . (9)
. (9)
Дата добавления: 2015-07-30; просмотров: 2282;
