Способы соединения потребителей электроэнергии

В трехфазной системе потребители электроэнергии соединя­ются звездой или треугольником. Передача электрической энер­гии от источника к потребителю в трехфазной трехпроводной системе осуществляется с помощью линейных проводов. В четы-рехпроводной трехфазной системе имеется четвертый — ней­тральный (Nn) провод, соединяющий общие точки фаз источника N и потребителя п.

Соединение, при котором концы всех трех фаз потребителя объединяют в общую точку п, называемую нейтральной точкой, а начала фаз подсоединяют к трехфазному источнику питания посредством линейных проводов, называется соеди­нением звездой трехфазного потребителя (рис. 2). Токи I_A, I_B и 1_C в соответствующих линейных проводах назы­ваются линейными, токи, протекающие по фазам, — фаз­ными, а ток I_N в нейтральном проводе — нейтральным. При рассмотрении трехфазной системы исходим из предполо­жения, что трехфазный источник является симметричным, фаз­ные напряжения которого равны между собой и сдвинуты по фа­зе относительно друг друга на угол 2п/3. Напряжения между линейными проводами потребителя Uab, Ubc и Uca называются линейными, а между началом и концом фаз потребителя, включенного звездой, U_A, U_B и U_C — фазными.

Из схемы рис. 2 видно, что при соединении потребителя звездой по его фазам протекают те же токи 1а, 1в и 1с, что и по линейным проводам. Это означает, что при соединении потреби­теля звездой фазные токи оказываются равными соответствую­щим линейным токам: I_Ф=I_л.

При этом по первому закону Кирхгофа для нейтральной точ­ки п можно записать

I_A+I_B+I_C=I_N.

При соединении потребителя звездой, независимо от величи­ны и характера сопротивлений его фаз, а также от того, имеется или отсутствует нейтральный провод, между линейными и фаз­ными напряжениями потребителя существуют следующие соот­ношения, полученные по второму закону Кирхгофа:

U_AB=Ua-Ub; U_BC=Ub-Uc, U_CA=Uc-Ua.

В большинстве практических случаев трехфазные потребите­ли представляют собой симметричную нагрузку, подключенную к симметричному трехфазному источнику питания.

Нагрузка, при которой комплексные сопротивления всех фаз потребителя равны между собой (Za=Zb=Zc), называется сим­метричной. При этом

R_a=R_b=R_c; Х_а=Хь=Хс, U_AB=U_BC=U_CA; U_A=u_B=u_C.

Сопротивления линейных проводов,
так же как и сопротивление нейтрально­
го, обычно малы и ими можно пренеб­
речь. При этом линейные напряжения
генератора равны линейным напряжени­
ям потребителя и соответственно фазные
напряжения генератора равны фазным л
напряжениям потребителя. В этом слу­
чае векторная диаграмма напряжений
потребителя будет совпадать с вектор­
ной диаграммой напряжений генерато­
ра. Исходя из полученных уравнений и Рис. 3

построений, можно сделать вывод о том,

что линейные напряжения потребителя,

так же как и фазные, сдвинуты относи­тельно

друг друга на угол 2л/3 (рис.3). На рис. 3—8. принято:

Za=Ra, Zb=Rb, Zc=Rc.

Из диаграммы следует, что при соединении потребителя элек­троэнергии звездой при симметричной нагрузке между фазными и линейными напряжениями существует соотношение:

U_л= U_Ф.

Фазные токи потребителя определяют по закону Ома:

I_A=U_a/Z_a, I_B=U_b/Z_b, I_C=U_c/Z_c.

При этом напряжение между нейтральными токами U_nN=0. Так как фазные напряжения и фазные сопротивления потребите­ля электроэнергии равны между собой, то фазные токи при сим­метричной нагрузке также равны между собой I_A=I_B=I_C=I_Ф и сдвинуты относительно фазных напряжений на равные углы φ_a= φ_b=φ_c=φ_ф , определяемые из выражений

tgφ_a=X_a/R_a= tgφ_b=X_b/R_b= tgφ_c=X_c/R_c

При симметричной нагрузке ток в нейтральном проводе, оп­ределяемый как векторная сумма фазных токов, оказывается рав­ным нулю, поэтому при симметричной нагрузке этот провод ста­новится не нужным и применять его нет смысла. При несимметричной нагрузке комплексные сопротивления всех трех фаз в общем случае не равны между собой, т. е. Z_a≠Z_b≠Z_c.

Пренебрегая сопротивлениями линейных проводов, можно считать, что линейные напряжения потребителя независимо от характера нагрузки равны соответствующим линейным напряже­ниям генератора, т. е. система линейных напряжений и при не­симметричной нагрузке симметрична.

При включении нейтрального провода и несимметричной на­грузке (сопротивлением нейтрального провода пренебрегаем) по­тенциал нейтральной точки потребителя п равен потенциалу ней­тральной точки N генератора. Следовательно фазные напряжения потребителя равны соответствующим фазным напряжениям гене­ратора, а напряжение между нейтральными точками U_nN=0.

При наличии нейтрального провода и несимметричной на­грузке геометрическая сумма фазных токов трехфазной системы в соответствии с первым законом Кирхгофа для нейтральной точки равна току в нейтральном проводе

I_A+I_B+I_C=I_N ≠0

При этом векторная диаграмма для несимметричной нагрузки с нейтральным проводом имеет вид, представленный на рис.4.

При отключении нейтрального провода потенциал нейтраль­ной точки п потребителя электроэнергии не равен потенциалу нейтральной точки N генератора при несимметричной нагрузке, так как эти точки не соединены между собой. При этом нейтраль­ная точка п на векторной диаграмме потребителя сместится из своего первоначального положения в другое (п’), при котором геометрическая сумма фазных токов потребителя равна нулю:

I_A+I_B+I_C=0.

В этом случае векторная диаграмма принимает вид представ­ленный на рис. 5, из которой следует, что при несимметричной нагрузке в трехфазной системе без нейтрального провода фазные напряжения потребителя оказываются не равными друг другу. При этом на одних фазах может быть пониженное напряжение по сравнению с фазными напряжениями генератора на других повышенное.

В этом случае между фазными токами, напряжениями и со­противлениями существуют те же соотношения, обусловленные законом Ома, что и при симметричной нагрузке.

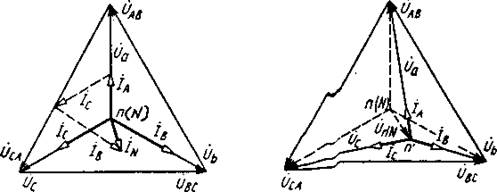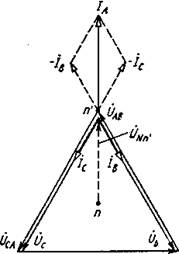
Рис.4 Рис. 5 Короткое замыкание одной фазы потребителя электроэнергии, соединенного звездой без нейтрального провода, следует рассмат­ривать как частный случай несимметричной нагрузки, при кото­ром напряжение на короткозамкнутой фазе потребителя становит­ся равным нулю, а напряжение на двух других фазах увеличивается до значений, равных линейным напряжениям (рис. 6). Нейтраль­ная точка п на векторной диаграмме смещается в этом случае в вер­шину треугольника линейных напряжений (и'), соответствующую короткозамкнутой фазе. При этом напряжение £/#«' между ней­тральными точками генератора и потребителя становится равным фазному напряжению питающего генератора.

Ток в короткозамкнутой фазе зависит от сопротивлений, вклю­ченных в двух других фазах потребителя. Геометрическая сумма векторов всех трех фазных токов в этом случае равна нулю.

Отключение нагрузки одной из фаз в трехфазной системе при соединении потребителя электроэнергии звездой без нейтрально­го провода можно также рассматривать как частный случай не­симметричной нагрузки, при которой сопротивление отключен­ной фазы равно бесконечности. При этом если сопротивления двух других фаз оказываются равными, то нейтральная точка п на векторной диаграмме переместится в середину одной из сто­рон треугольника (п) линейных напряжений (рис. 7). При обрыве линейного провода трехфазный потребитель на­ходится под линейным напряжением, так как при этом ни одна из точек нагрузки не будет под потенциалом оборванного линейного провода. В этом случае векторная диаграмма трехфазного по­требителя при соединении звездой и отсутствии нейтрального провода приобретает вид, представленный на рис. 8.

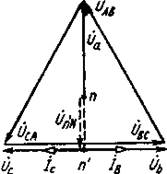Рис.6

Рис.7

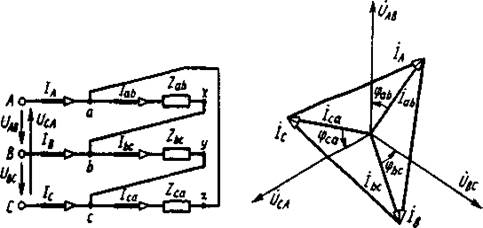Рис.9 Рис. 10

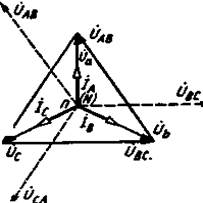
Соединение, при котором конец первой фазы х соединяется с началом второй b, конец второй у — с началом третьей с, а конец третьей z — с началом первой а, называется соединением трехфазного потребителя электрической энер­гии треугольником. При этом начала всех фаз потребите­ля присоединяют к источнику электрической энергии с помощью линейных проводов. Из рис. 9 видно, что каждая фаза потреби­теля присоединяется соответственно к двум линейным проводам. Поэтому при соединении потребителя треугольником фазные на­пряжения оказываются равными соответствующим линейным на­пряжениям: U_Ф-U_Л. Фазные токи при соединении трехфазного потребителя треугольником не равны линейным, так как в нача­ле каждой фазы потребителя имеется узел разветвления токов. При этом независимо от сопротивлений потребителя между фаз­ными и линейными токами существуют соотношения, получен­ные на основании первого закона Кирхгофа для узлов разветвле­ния токов:

I_A=I_ab-I_ca; I_B=I_bc-I_ab; I_C=I_ca-I_bc.

Пользуясь указанными соотношениями, по векторам фазных токов, I_ab, I_bc, I_ca можно построить векторы линейных токов I_A, I_B, I_C,

Соотношения между фазными напряжениями, токами и со­противлениями при соединении потребителя треугольником на­ходят в соответствии с законом Ома: I_ab=U_AB/Z_ab, I_bc=U_BC/Z_bc,

I_ac=U_AC/Z_ac. На рис. 5.10,5.13 принято: Z_ab=R_ab, Z_bc=R_bc, Z_ac=R_ac,

Углы сдвига по фазе между векторами фазных напряжений, U_AB, U_BC, U_AC, и соответствующих фазных токов I_ab, I_bc, I_ac опреде­ляются фазными сопротивлениями потребителя:

φ_bc=arctgX_ab/R_ab, φ_bc=arctgX_bc/R_bc, φ_ac=arctgX_ac/R_ac.

При симметричной нагрузке комплексные сопротивления всех трех фаз одинаковы, т. е. Z_ab=Z_bc=Z_ac. При этом как актив­ные, так и реактивные сопротивления фаз потребителя равны: R_ab=R_bc=R_ac, X_ab=X_bc=X_acпричем реактивные сопротивления имеют одинаковый (индуктивный или емкостный) характер. В этом случае фазные токи и соответствующие углы сдвига по фа­зе между фазными напряжениями и фазными токами будут равны между собой: I_ab=I_bc=I_ac=I_ф, φ_ab=φ_bc=φ_ac=φ_ф

Таким образом, при соединении трехфазного потребителя электроэнергии треугольником при симметричной нагрузке токи всех трех фаз равны между собой и сдвинуты относительно соот­ветствующих линейных напряжений на одинаковые углы. Из век­торной диаграммы для симметричной нагрузки при соединении потребителя треугольником, представленной на рис..10, видно, что линейные токи оказываются равными и сдвинутыми относи­тельно друг друга по фазе на угол 2п/3. При этом между фазными и линейными токами существует соотношение:

I_л=√3I_ф.

При несимметричной нагрузке фазные токи и углы сдвига по фазе между фазными токами и фазными напряжениями в общем случае не одинаковы. Так же как и при симметричной нагрузке, они могут быть определены по соответствующим формулам. Ли­нейные токи и в этом случае определяются через соответствую­щие фазные токи. Векторная диаграмма, построенная для случая несимметричной активной нагрузки трехфазного потребителя при соединении треугольником, представлена на рис..11.

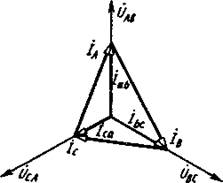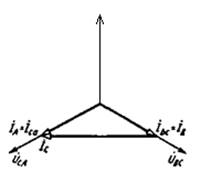Рис.11 Рис.12

Отключение нагрузки одной из фаз сле-

дует рассматривать как частный случай не-

симметричной нагрузки, когда сопротиление

отключенной фазы равно бесконечности. В

этом случае векторная диаграмма приобре-

тает вид, представленный на

(Z_ab=∞). Рис. 13

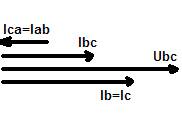
При обрыве линейного провода в цепи трехфазного потребителя электроэнергии, соединенного треуголь­ником, следует рассматривать его как потребителя, подключенно­го к однофазному источнику (U_ab)- Векторная диаграмма токов и напряжений для этого случая представлена на рис.13.

Активную мощность трехфазного потребителя электроэнер­гии в общем случае можно определить как сумму активных мощ­ностей всех его фаз:

при соединении звезоой

Р=Р_a+Р_b+Р_c= UaIaCOS φ_a + UbIbCOS φ_b + UcIcCOS φ_c

при соединении треугольником

Р=Р_ab+Р_bc+Р_ca= UabIabCOS φ_ab + UbcIbcCOS φ_bc + UcaIcaCOS φ_ca

При симметричной нагрузке фазные напряжения, токи и уг­лы сдвига фаз оказываются равными. Вследствие этого равны также и активные мощности всех трех фаз потребителя электро­энергии.

Активная мощность трехфазного потребителя независимо от схемы его соединения может быть найдена через линейные токи и напряжения:

P=3P_ф=3U_фI_фcos φ_ф=√3U_лI_лcos φ_ф или P=√3UIcos φ

Аналогично можно получить и формулу для реактивной мощности трехфазного потребителя при симметричной на­грузке:

Q=√U_лI_лsin φ_ф или Q=√3UIsin φ

Полная мощность трехфазного потребителя при симметрич­ной нагрузке:

S=√P²+Q²=3U_лI_л или S=√3UI.

Задание по работе

1. Исследовать трехпроводную трехфазную электрическую цепь при соединении потребителей электроэнергии звездой и ус­тановить соотношения между линейными и фазными токами I_л и I_ф и напряжениями U_л и U_ф при симметричном и несимметричном режимах работы.

2. Исследовать четырехпроводную трехфазную цепь при со­единении потребителей звездой и установить соотношения между линейными и фазными токами и напряжениями при симметрич­ном и несимметричном режимах работы.

3. Исследовать трехфазную цепь при соединении потребите­лей треугольником и установить соотношения между линейными и фазными токами и напряжениями.

4. Для исследуемых цепей построить векторные диаграммы токов I и напряжений U при симметричном и несимметричном режимах работы.

5. Составить краткие выводы по работе.