Термодинамическое разрушение мерзлых рыхлых и связных пород путем оттаивания и абляции

Режим термодинамического разрушения мерзлых рыхлых и связных пород путем оттаивания и абляции имеет место при T_Th < 10⁶°С/м в процесс бурения скважин или очистки добычного и транспортного горного оборудования от намерзшей горной массы. Этот режим разрушения будет устойчив в том случае, когда скорость истечения теплоносителя будет достаточной для создания динамического давления, при котором бы обеспечивались отрыв оттаявших с поверхности агрегатных частиц горной массы и их удаление (абляция).

Применительно к очистке металлических рабочих поверхностей добычного и транспортного оборудования от намерзшей горной ассы термодинамическое разрушение путем оттаивания и абляции будет только в начальный период. В последующем, когда за счет оттаивания и абляции примерзшая горная масса будет разрушена до металлической рабочей поверхности добычного или транспортного оборудования, механизм разрушения будет иной. В этом случае оттаивание и абляция по контакту «металл - примерзший слой горной массы» будет происходить более интенсивно (так как теплопроводность металла примерно на порядок выше теплопроводности породы), чем в объеме мерзлой рыхлой или связной породы. При этом разуется кольцевой клин (рис. 5.2), который создает благоприятные условия для разрушения крупными кусками, образующимися в результате излома по контуру кольцевой консоли, представленной мерзлой горной массой.

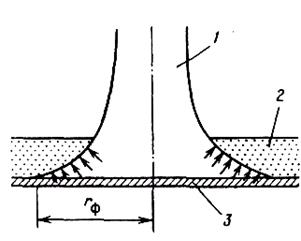
Рис 5.2. Схема к расчету параметров термодинамической очистки металлических поверхностей добычного и транспортного оборудования от намерзшей горной массы:

1 — высокоскоростная газо­вая струя; 2 — промерзший слой горной массы; 3 — металлическое основание

Для аналитического описания процесса термодинамического разрушения мерзлых рыхлых и связных пород путем оттаивания и абляции их можно представить как твердые агрегатные частицы, равномерно распределенные в объеме льда.

Выражение для оценки линейной скорости V_л (м/с) термодинамического разрушения мерзлых рыхлых и связных пород путем оттаивания и абляции агрегатных частиц можно представить в виде

V_л = V_пл К, (5.18)

где V_пл— скорость плавления льда с абляцией, м/с; К — коэффициент, характеризующий отличие механизма термодинамического разрушения мерзлых рыхлых и связных пород от механизма разрушения льда; для пес­ков К ~ 0,8÷0,9, супесей К ~ 0,3÷0,5, суглинков К = 0,05÷0,1, глин К = (0,3÷1)10^-2.

Для определения скорости V_пл рассмотрим одномерную задачу плавления полуограниченного стержня с теплоизолированной боко­вой поверхностью, или, что то же самое, одномерную задачу плавле­ния полуограниченного пространства. Тепловую модель процесса можно представить следующим образом: полупространство или по­луограниченный стержень Z > 0 имеет начальную температуру мер­злых рыхлых или связных пород, равную Т₀; в момент времени τ = 0 на поверхность полупространства начинает действовать газовый теп­лоноситель с температурой Т_т, теплообмен осуществляется по закону конвекции. В момент начала плавления τ_пл температура поверхности полупространства станет равной температуре фазового перехода лед-вода Т_ф. Если считать, что расплав будет удаляться, то из физи­ческих соображений следует, что температура поверхности полупро­странства при тепловом воздействии поддерживается постоянной равной Т_ф. При такой постановке процесс разрушения льда можно рассматривать состоящим из двух этапов: нагрева поверхности от Т₀ до Т_ф без абляции и последующего нагрева с плавлением и абляцией.

Для нахождения времени τ_пл, необходимо решить дифференци­альное уравнение

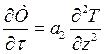(5.19)

при начальном условии

T(z, 0) = T₀ (5.20)

и граничных условиях

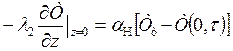(5.22)

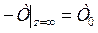(5.22)

где a₂— температуропроводность мерзлой рыхлой или связной породы, м/с; 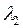— теплопроводность, Вт/(м²·°С); 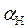— коэффициент теплоотдачи при нагреве теплоносителем мерзлой горной породы, Вт/(м²·°С).

Общее решение дифференциального уравнения (5.19) при кра­евых условиях (5.20)-(5.2) имеет вид

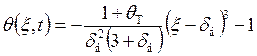(5.23)

где 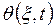—безразмерная текущая температура, 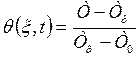; 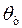— безразмерная температура теплоносителя, 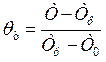; ξ— безразмерная текущая координата, 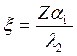;t — безразмерное текущее время, 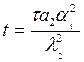; δ_б — безразмерная координата, до которой наблюдается влия­ние нагрева поверхности, 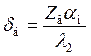; Z_B — размерная координата, до которой наблюдается влияние нагрева поверхности.

Величина δ_б зависит от времени и находится из трансцендент­ного уравнения

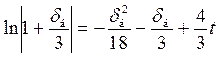(5.24)

При τ = τ_пл ; Т(0,τ_пл) = Т_ф, а θ(0,t_пл) = 0 (где t_пл — безразмер­ное время начала плавления поверхности полупространства, )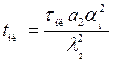

Подставляя θ(0,t_пл) = 0 в (5.23), получим

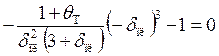
откуда

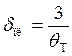(5.25)

где 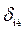— безразмерная координата, до которой наблюдается вли­яние нагрева поверхности, когда ее температура стано­вится равной Т_ф.

Подставляя (5.25) в (5.24), получим выражение для оценки безразмерного времени начала плавления поверхности полупрост­ранства

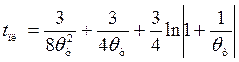(5.26)

С учетом (5.26) размерное время начала плавления поверхно­сти полупространства будет

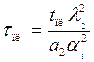(5.27)

Начиная с τ = 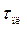происходит плавление полупространства с удалением продуктов плавления (с абляцией).

Для аналитического описания процесса плавления с абляцией необходимо решить уравнение теплопроводности (5.19) при следу­ющих граничных условиях

T│_z=Z= Т_ф; (5.28)

Т│_z=∞ = Т₀; (5.29)

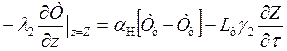(5.30)

где Z = f(τ) - координата фронта плавления, м; L_ф — скрытая теплота плавления льда, Дж/кг; ^γ₂ — плотность материала, кг/м³.

Если ввести дополнительно безразмерные величины

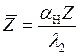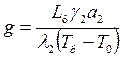и (5.31)

то дифференциальное уравнение

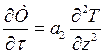
и граничные условия

Т│_z=∞ = Т₀;

,

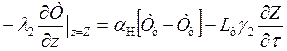соответственно принимают вид

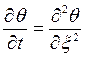(5.32)

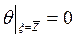(5.33)

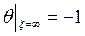(5.34)

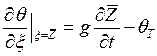(5.35)

Решение уравнения (5.32) при граничных условиях (5.33) и (5.34) имеет вид

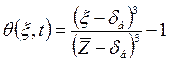(5.36)

Дифференцируя это выражение по ξ, получим

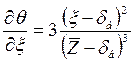(5.37)

откуда при 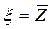, получим

(5.38)

Подставляя (5.38) в (5.35), получим

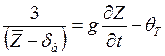(5.39)

Интегрируя уравнение (5.32) в пределах от 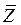до 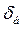, получим

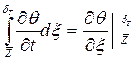(5.40)

Известно, что

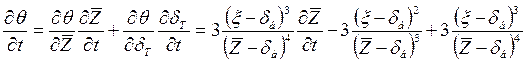(5.41)

Подставляя (5.41) в (5.40) и принимая во внимание (5.36), получим

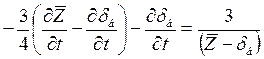(5.42)

С учетом того, что выражение (5.42) принимает вид

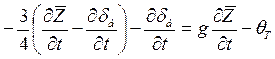
или

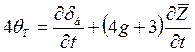(5.43)

Решая совместно уравнения (5.39) и (5.43) пр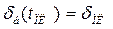и и 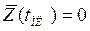, получим

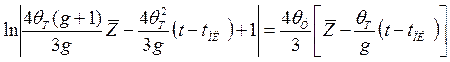(5.44)

Из этого трансцендентного можно определить безразмерную координату фронта плавления .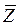

Продифференцировав выражение (5.44) по t можно определить скорость продвигания фронта плавления

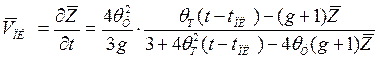(5.45)

Если g>>1, то для практических расчетов с достаточной точностью вместо формулы (5.45) можно использовать упрощенную формулу

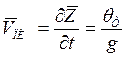(5.46)

Размерная скорость подвигания фронта плавления определяет­ся из выражения

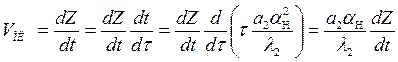
или

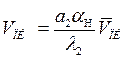(5.47)

Таким образом, скорость разрушения мерзлых рыхлых и связ­ных пород путем оттаивания с абляцией на основании (5.18) и с учетом (5.47) будет

(5.48)

или для приближенных расчетов

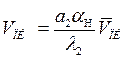(5.49)

Зависимости (5.48) и (5.49) справедливы для оценки линей­ной скорости термодинамического разрушения мерзлых рыхлых и связных пород применительно к бурению в них скважин. Примени­тельно к очистке добычного и транспортного горного оборудования от намерзшей горной массы эти зависимости справедливы для оценки скорости разрушения только лишь на первой стадии, когда фронт очистки еще не достиг металлической рабочей поверхности оборудо­вания. После того как фронт разрушения достигнет металлической рабочей поверхности оборудования, изложенный выше механизм разрушения будет сочетаться с крупным сколом мерзлой горной мас­сы вокруг кольцевого клина (см. рис. 5.2). При этом в пространство кольцевого клина попадает газовый поток и создает избыточное дав­ление Р_и, Па

Р_и=0,5γ_тU_r². (5.50)

За счет избыточного давления на смерзшуюся горную массу, находящуюся над кольцевым клином, действует изгибающий момент F_и

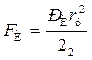(5.51)

где r_ф — текущий радиус на контакте «металлическая поверх­ность-примерзшая горная масса», где выполняется усло­вие Т = Т_ф, м.

Величину r_ф можно определить из решения дифференциаль­ного уравнения теплопроводности применительно к распростране­нию тепла в пластине при ее нагреве с торца. По мере роста r_ф изгибающий момент Р_и возрастает и при некотором критическом его значении происходит скол мерзлой горной массы по кольцевому кли­ну. Величина r_ф, при которой произойдет скол, определяется из ус­ловия

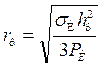(5.52)

где h_м — толщина примерзшего слоя горной массы, м; σ_и — предел прочности примерзшей горной массы на изгиб, Па.