Классификация типов механического движения

Мехатронные устройства предназначены, как отмечалось, для перемещения рабочих органов машин и других объектов в соответствии с назначением этих машин. Требуемое механическое движение можно классифицировать по различным признакам:

1. По функциональному назначению движения:

– механические движения для выполнения основных и вспомогательных операций в технологических и энергетических машинах;

– механические движения движителей транспортных средств;

– механические движения исполнительных органов систем управления.

2. По типу движения:

– плоское движение, когда все точки объекта перемещаются в одной или параллельной плоскостях;

– пространственное движение, когда движущийся объект имеет точки, траектории движения которых не лежат в одной или в параллельных плоскостях.

3. По характеру движения в плоскости:

– вращательное движение;

– поступательно движение;

– сложное (плоскопараллельное) движение, обычно получаемое в результате сложения простых движений.

4. По скоростному режиму:

4.1. Однонаправленное движение:

– однонаправленное движение с постоянной скоростью;

– однонаправленное движение с переменной скоростью;

– однонаправленное движение с мгновенными остановками в некоторых промежуточных положениях;

– однонаправленное движение с остановами конечной продолжительности в некоторых промежуточных положениях;

– однонаправленное движение с остановками конечной продолжительности и с мгновенными остановками в некоторых промежуточных положениях;

4.2. Разнонаправленное (реверсивное) движение:

– реверсивное движение с мгновенными остановками в момент смены направления движения;

– реверсивное движение с остановками конечной продолжительности между периодами движения объекта в разных направлениях;

– реверсивное комбинированное движение, когда между периодами движения в разных направлениях могут быть остановки как конечной продолжительности, так и мгновенной.

4.3. Комбинированное движение объекта, когда в отдельные периоды времени объект совершает все возможные варианты однонаправленного движения, а в другие – все возможные варианты реверсивного движения.

Для характеристики скоростного режима движения объекта обычно используются временные диаграммы для угловых j(t) и линейных S(t) перемещений, а также временные диаграммы для угловых w(t) и линейных V(t) скоростей. В качестве примера на рис. 234 приведены диаграммы для реверсивного комбинированного движения.

5. По периодичности смены режимов движения:

– апериодичные движения, когда изменение скоростей при однонаправленном движении и изменение направления движения объекта при реверсивном движении, а так же остановки, происходят апериодически, т.е. не являются циклическими;

– периодические движения объекта с циклическим повторением отдельных этапов движения; циклические движения характеризуются длительностью цикла и величиной перемещения за цикл.

6. По способу задания траектории движения в пространстве и во времени:

– позиционное, когда траектория движения объекта задается отдельными точками позиционирования, при этом объект имеет остановки в каждой точке позиционирования;

– контурное задание траектории движения, когда траектория движения определяется бесконечно большим числом ее точек.

При позиционном задании целью движения объекта является перемещение в точку пространства с заданными координатами. Это перемещение обеспечивается движением объекта по каждой координате пространства перемещений. Движения по координатам при этом не связаны друг с другом, что порождает неопределенность траектории и скорости движения. Случай позиционного управления поясняется на рис. 235, а).

Для перемещения объекта из точки 1 в точку 2 его перемещают по координате X на величину 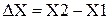, а по координате Y – на величину 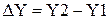. Эти перемещения могут быть как одновременными, так и последовательными. Их результатом является перемещение объекта из точки 1 в точку 2 по неопределенной траектории.

При контурном задании перемещений движение объекта между точками 1 и 2 должно осуществляться по требуемой траектории. Это движение обеспечивается одновременными взаимосвязанными перемещениями по всем координатам пространства перемещений (рис. 235, б). Требуемая траектория движения разбивается базовыми точками bi на небольшие отрезки, в пределах которых криволинейная траектория аппроксимируется (с допустимой погрешностью) более простыми зависимостями (линейной или круговой). Движение объекта осуществляется поочередными небольшими шагами вдоль управляемых координат перемещений так, чтобы отклонения от заданной траектории были б минимальными.

7. По плавности диаграмм скоростей и ускорений:

– движение с «жесткими» ударами (диаграмма скоростей имеет разрывы конечной величины);

– движение с «мягкими» ударами (диаграмма ускорений имеет разрыв конечной величины);

– движение безударное (диаграммы скоростей и ускорений не имеют разрывов).

8. По типу диаграмм ускорений (в качестве примера упомянуты наиболее известные законы):

– гармонический закон изменения ускорений;

– закон движения «постоянное ускорение»;

– закон движения «равноубывающее ускорение»;

– косинусоидальный закон изменения ускорения;

– закон движения «наклонная синусоида»;

– тригонометрический закон Тира;

– закон Шуна.