Синтез кинематической модели мехатронной системы

Кинематическая модель мехатронного устройства во многом определяет его качество. Разработку кинематической модели (кинематической схемы) мехатронного устройства можно вести в соответствии со следующим алгоритмом:

1. Анализ возможных путей решения задачи.

2. Синтез кинематической модели мехатронного модуля.

3. Синтез кинематической модели мехатронного устройства.

3.1. Синтез структурной схемы мехатронного устройства;

3.2. Описание мехатронного устройства уравнениями кинематики (например, аналитическими зависимостями, описывающими решения прямой задачи манипуляторов роботов);

3.3. Оценка качества кинематической схемы мехатронного устройства по соответствующим критериям.

4. Решение обратной задачи кинематики мехатронного устройства.

5. Разработка кинематической модели систем разгрузки звеньев мехатронного устройства.

При решении задачи синтеза кинематической модели мехатронного модуля учитывается специфика последнего, заключающаяся в возможности выполнения многих функций модуля как структурными, так и программными средствами.

Мехатронный модуль служит для обеспечения заданного закона перемещения ВМЗ путем создания с помощью системы управления необходимого закона движения силового элемента. В наиболее общем виде мехатронный модуль можно представить схемой, изображенной на рис. 231, где СЭ – силовой элемент, МПиПД – механизм преобразования и передачи движения; РО – рабочий орган мехатронного модуля; w_Д(t) – угловая скорость вала двигателя; w_р и V_р – угловая или линейная скорость рабочего органа; t – время.

В зависимости от сложности заданного закона движения рабочего органа и от назначения мехатронного модуля функции получения и преобразования движения могут быть различным образом распределены между системой управления мехатронного модуля и механизмом преобразования и передачи движения. Наиболее характерными являются следующие три случая:

1) закон движения рабочего органа полностью обеспечивается системой управления;

2) закон движения полностью обеспечивается механизмом преобразования и передачи движения;

3) закон движения обеспечивается совместно системой управления и механизмом передачи и преобразования движения.

В первом случае передаточное отношение i_M механизма преобразования и передачи движения должно быть постоянным.

Пример 1. Пусть необходимо перемещать рабочий орган возвратно-поступательно по гармоническому закону

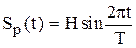; 0 £ t £ T,

при условии использования в механизме преобразования и передачи движения передачи винт-гайка с шагом h (здесь H – амплитуда колебания (перемещения) рабочего органа, м; Т – период колебаний, с).

Передаточное отношение i_M механизма преобразования и передачи движения можно определить как отношение скоростей его входного вала и рабочего органа или как отношение перемещений этих звеньев за единицу времени. Так как за один оборот входного вала рабочий орган в механизме винт-гайка перемещается на величину шага h, то

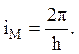
Установим закон изменения линейной скорости рабочего органа, продифференцировав выражение для :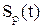

,

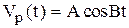где ; .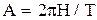

Примем Н = 0,05 м; Т = 10 с; h = 0,005 м. Положим, что вал электродвигателя соединен через муфту непосредственно с валом ходового винта,

тогда

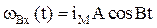
или

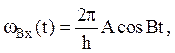
где ω_Вх – угловая скорость входного звена механизма преобразования и передачи движения – в данном случае вала ходового винта.

Закон углового перемещения j_Вх(t) вала винта определяется интегрированием последнего выражения:

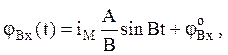
где j_Вх^o – начальное положение вала ходового винта.

Определим некоторые параметры данного закона движения, а именно:

· максимальное значение угловой скорости вала винта

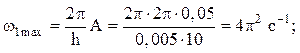
· амплитуда перемещений вала ходового винта (определяется путем интегрирования выражения для ω_Вх(t) на интервале 0 £ t £ 0,25 T)

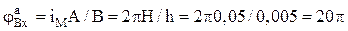рад.

Таким образом, при реализации заданного закона движения вал ходового винта должен иметь амплитуду колебаний угла поворота, равную 10 оборотам, и менять скорость от нуля до примерно 40 с^–1 в прямом и обратном направлениях. Если указанные диапазоны изменения параметров двигателя по каким-либо соображениям не устраивают разработчика, их можно пропорционально увеличить или уменьшить, предусмотрев в механизме преобразования и передачи движения понижающую или повышающую передачу (например, зубчатую).

Система управления в этом случае должна обеспечить необходимое значение крутящего момента на валу с учетом действительной скорости и положения рабочего органа.

Во втором случае, в отличие от первого, угловая скорость вала двигателя может быть постоянной.

Пример 2. Пусть для обеспечения гармонического закона движения используется синусный механизм (рис. 232), входящий в состав механизма преобразования и передачи движения и реализующий функцию

,

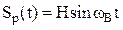где w_В = 2p/T – угловая скорость входного вала синусного механизма; Н – длина входного звена данного механизма, равная требуемоемой амплитуде перемещения рабочего органа.

Так как кинематика синусного механизма обеспечивает синусоидальный закон движения рабочего органа при w_В = const, то вал двигателя также должен иметь постоянную угловую скорость w_д. Если в этом случае принять, что вал двигателя и вал синусного механизма соединены муфтой, то при
Т = 10 с w_В = w_д = 0,2 p с^-1 .

Задачей системы управления двигателем в рассматриваемом случае будет обеспечение пуска двигателя и стабилизация его скорости (если необходимо) при изменяющейся во времени нагрузке на рабочий орган.

В третьем случае заданное движение рабочего органа обеспечивается совместно механизмом преобразования движения и системой управления. При этом возникает задача рационального распределения функций обеспечения заданного закона движения между механизмом преобразования движения и системой управления. Наиболее типичным является подход, когда предварительно выбирается передаточное отношение i_M(t) механизма преобразования движения, а затем рассчитывается требуемый закон движения вала двигателя, который обеспечивается системой управления двигателем.

Пример 3. Спроектировать мехатронный модуль, реализующий движение точки А выходного механического звена 2 по траектории L(x, y, t), являющейся участком кардиоиды (рис. 233). Пусть перемещение этой точки в интервале изменения угла j_M входного звена 1 от -0,75p до +0,75 p происходит с постоянной скоростью V_A. Движение обеспечивается за счет вращения кривошипа 1. Предполагается, что движение точки А вне указанных границ изменения угла j_M осуществляется по другому закону, который здесь не рассматривается.

Запишем параметрические уравнения движения точки А как функции угла j_M поворота входного звена механизма:

x = l₁ + l₁ cos j_M - l₂ cos 0,5 j_M;

y = l₁ sin j₂ - l₂ sin 0,5 j_M.

Получим уравнения для скоростей:

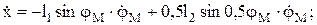
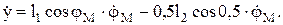
Абсолютная скорость точки А

.

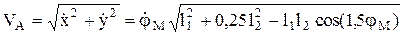Тогда

.

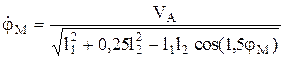Здесь 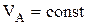и задается в зависимости от требований реализуемого технологического процесса.

Последнее выражение является обыкновенным дифференциальным уравнением первого порядка и отражает зависимость угловой скорости вала механизма от его угловой координаты j_M, т.е. 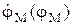. Для решения задачи управления необходимо иметь законы изменения скорости 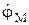и угла j_M во времен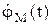и: и .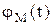

Чтобы получить эти зависимости, можно воспользоваться, например, разностной схемой Эйлера и решить задачу численно. Вначале определить функцию 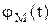по рекуррентной формуле

,

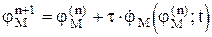а затем функцию 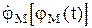. Здесь t – малое приращение времени (шаг решения). Расчет следует начинать с .

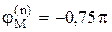Если между валом двигателя и входным валом рассматриваемого механизма имеется передача с передаточным отношением i_М, то

.

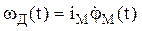Максимальное значение 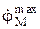угловой скорости должно быть обеспечено системой управления при j_M = 0, а минимальное 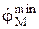– при 2p/3.

;

.

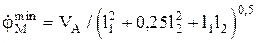Пусть V_A = 1 м/с; l₁ = 0,1 м; l₂ = 0,25 м.

Тогда

;

.

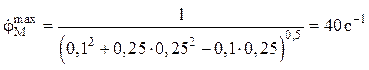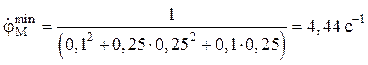Таким образом, задача проектирования мехатронного устройства имеет многие варианты решения, которые отличаются, в частности, распределением функций между его электронной и механической частями, степенью гибкости спроектированного устройства, его сложностью и стоимостью.