Основные формулы и законы. · Волновые функции связанных состояний (Е < 0) атома водорода имеют вид
· Волновые функции связанных состояний (Е < 0) атома водорода имеют вид
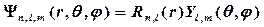 ,
,
где 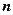 – главное квантовое число (
– главное квантовое число ( 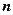 = 1, 2, 3, …);
= 1, 2, 3, …); 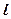 – орбитальное (азимутальное) квантовое число (
– орбитальное (азимутальное) квантовое число ( 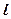 = 0, 1, 2, …, (
= 0, 1, 2, …, ( 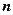 – 1));
– 1));
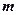 – магнитное квантовое число (
– магнитное квантовое число ( 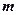 = 0, ±1, ±2, …, ±
= 0, ±1, ±2, …, ± 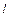 );
); 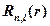 – радиальные функции, а
– радиальные функции, а 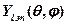 – сферические функции.
– сферические функции.
Квантовые числа 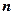 ,
,  ,
, 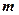 являются характеристиками микросостояния частицы, в том числе и электрона в атоме водорода, и появляются при решении нерелятивистского уравнения Шредингера.
являются характеристиками микросостояния частицы, в том числе и электрона в атоме водорода, и появляются при решении нерелятивистского уравнения Шредингера.
· Квантовое магнитное спиновое число 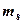 (
( 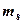 =±1/2) электрона появляется лишь при решении релятивистского уравнения Дирака, т. е. спин является релятивистской характеристикой.
=±1/2) электрона появляется лишь при решении релятивистского уравнения Дирака, т. е. спин является релятивистской характеристикой.
· Принцип Паули: в атоме два электрона не могут находиться в одном и том же квантовом состоянии (определяемом набором четырех квантовых чисел 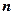 ,
,  ,
, 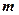 ,
, 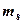 ).
).
· Электронная конфигурация атома в основном состоянии 1s2 2s2 2p6 3s2 3p6 3d10…, где числа ( 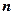 = 1, 2, 3, …) соответствуют главному квантовому числу, которое задает электронные слои (оболочки) K, L, M, N, …. Буквы латинского алфавита s, p, d, f соответствуют орбитальному квантовому числу (
= 1, 2, 3, …) соответствуют главному квантовому числу, которое задает электронные слои (оболочки) K, L, M, N, …. Буквы латинского алфавита s, p, d, f соответствуют орбитальному квантовому числу (  = 0, 1, 2, 3), которое задает s, p, d, f – состояния (электронные подоболочки) атома. Числа над s, p, d, f соответствуют числу электронов в соответствующих состояниях.
= 0, 1, 2, 3), которое задает s, p, d, f – состояния (электронные подоболочки) атома. Числа над s, p, d, f соответствуют числу электронов в соответствующих состояниях.
· Закон Мозли
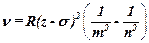 ,
,
где 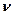 – характеристические частоты спектра;
– характеристические частоты спектра; 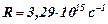 – постоянная Ридберга;
– постоянная Ридберга; 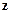 – заряд ядра атома в относительных единицах;
– заряд ядра атома в относительных единицах; 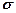 – постоянная экранирования;
– постоянная экранирования; 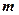 и
и 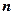 – квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.
– квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.
· При 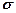 = 0 формула закона Мозли обращается в формулу, описывающую линейчатые спектры водородоподобных атомов
= 0 формула закона Мозли обращается в формулу, описывающую линейчатые спектры водородоподобных атомов
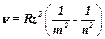 .
.
При 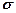 = 0 и
= 0 и 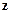 = 1 формула закона Мозли совпадает с обобщенной формулой Бальмера для линейчатого спектра атома водорода.
= 1 формула закона Мозли совпадает с обобщенной формулой Бальмера для линейчатого спектра атома водорода.
· Частоты излученного или поглощенного электромагнитного кванта молекулярного спектра
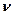 =
= 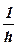 (∆ Wэл. + ∆ Wкол. + ∆ Wвр.),
(∆ Wэл. + ∆ Wкол. + ∆ Wвр.),
где ∆Wэл., ∆Wкол. и ∆Wвр. – разности энергий двух соответственно электронных, колебательных и вращательных уровней.
· Средняя энергия квантового одномерного осциллятора
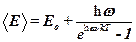 ,
,
где 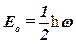 – нулевая энергия;
– нулевая энергия; 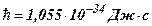 - постоянная Планка;
- постоянная Планка; 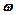 – циклическая частота колебаний осциллятора;
– циклическая частота колебаний осциллятора; 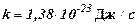 – постоянная Больцмана;
– постоянная Больцмана;
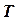 – термодинамическая температура.
– термодинамическая температура.
· Молярная внутренняя энергия системы, состоящей из невзаимодействующих квантовых осцилляторов
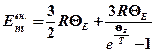 ,
,
где 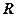 – молярная газовая постоянная;
– молярная газовая постоянная; 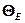 =
= 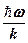 – характеристическая температура Эйнштейна.
– характеристическая температура Эйнштейна.
· Молярная теплоемкость кристаллического твердого тела в области низких температур (предельный закон Дебая)
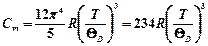 ( T <<
( T << 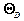 ),
),
где 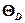 =
= 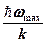 – характеристическая температура Дебая.
– характеристическая температура Дебая.
· Распределение свободных электронов в металле по энергиям при 0 К
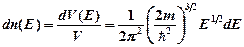 ,
,
где 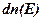 – концентрация электронов, энергия которых заключена в пределах от
– концентрация электронов, энергия которых заключена в пределах от 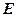 до
до 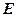 +
+ 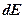 ;
; 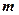 – масса электрона. Это выражение справедливо при
– масса электрона. Это выражение справедливо при 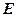 <
< 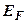 (
( 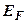 – энергия или уровень Ферми).
– энергия или уровень Ферми).
· Энергия Ферми в металле при Т = 0 К
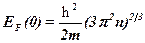 ,
,
где 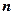 – концентрация электронов в металле.
– концентрация электронов в металле.
· Средняя энергия электронов
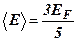 .
.
· Удельная проводимость собственных полупроводников
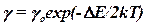 ,
,
где 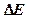 – ширина запрещенной зоны;
– ширина запрещенной зоны; 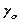 - константа.
- константа.
· Сила тока в p-n – переходе
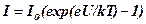 ,
,
где 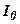 – предельное значение силы обратного тока;
– предельное значение силы обратного тока;
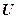 – внешнее напряжение, приложенное к p-n – переходу.
– внешнее напряжение, приложенное к p-n – переходу.
· Связь между глубиной 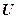 потенциальной ямы и работой выхода
потенциальной ямы и работой выхода 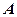 из металла и полупроводника:
из металла и полупроводника:
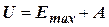 ,
,
где 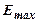 – максимальная энергия электрона в яме.
– максимальная энергия электрона в яме.
· Внутренняя контактная разность потенциалов
 ,
,
где 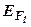 и
и 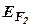 - энергия Ферми соответственно для первого и второго металла или полупроводника;
- энергия Ферми соответственно для первого и второго металла или полупроводника; 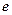 – заряд электрона.
– заряд электрона.
Дата добавления: 2015-07-30; просмотров: 1036;
