Конструирование конической передачи редуктора

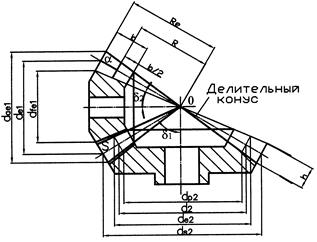
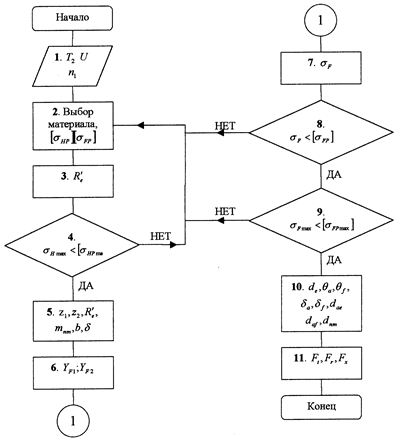
Проектировочный расчет закрытых конических передач (рис. 10) проводится по условию контактной выносливости активных поверхностей зубьев для предотвращения их усталостного выкрашивания. Схема алгоритма расчета конической передачи редуктора представ­лена на рис. 11.

Рис. 10. Геомет­рические парамет­ры конической зубчатой передачи

2.3.1. Описание блок-схемы расчета

конической передачи редуктора

Исходные денные:

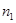- частота вращения шестерни, об/мин;

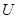- передаточное число конической передачи;

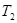- крутящий момент на колесе конической передачи, Н×мм.

Рис. 11. Блок-схема расчета конической передачи редуктора

1. Выбрать материал зубчатой передачи и определить допускаемое контактное напряжение и допускаемые напряжения изгиба (см. § 2.1).

2. Определить внешнее конусное расстояние конической передачи

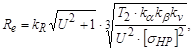мм,

где 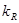- вспомогательный коэффициент. При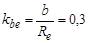

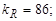
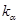- коэффициент распределения нагрузки между зубьями. Для прямозубых передач 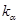= 1;

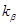- коэффициент, учитывающий распределение нагрузки по ширине венца. Для прирабатывающихся колес (материалы 1-й группы) с прямыми зубьями 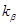=1. Для колеса с НВ>350 (материалы 2-й группы) 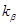= 1,12,...,1,42 при изменении передаточного числа 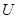=2,5,...,6,3;

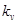- коэффициент динамической нагрузки. Для 6-8-й степени точности рекомендуется принимать для прямозубых передач:

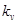= 1,1 при n₁ < 2000 об/мин;

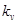= 1,15 при n₁ > 2000 об/мин.

3. Провести проверку передачи на контактную прочность при дей­ствии максимальной нагрузки (см. § 2.2, п. 9-11).

4. Определить геометрические размеры колес:

а) определить число зубьев колеса 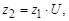где 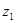- число зубьев шестерни. Для скоростных передач 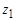=20,…,30, для тихоходных 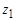=17,…,24;

б) определить ориентировочное значение внешнего окружного мо­дуля

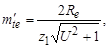мм.

Полученное значение модуля округлить до ближайшего большего значе­ния 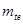по ГОСТ 9563-60 (см. табл. 18);

в) по выбранному 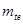провести уточнение внешнего конусного рас­стояния

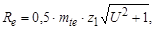мм;

г) определить модуль на середине ширины зуба

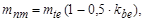мм;

д) определить рабочую ширину зацепления и углы при вершинах конусов

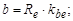
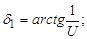
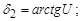мм.

5. Определить коэффициенты формы зуба и 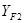по эквивалент­ному колесу (см. табл. 19):

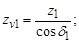
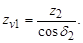
6. Для наиболее слабого звена определить напряжения изгиба в ножке зуба. Слабое звено определяется минимумом соотношения

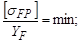
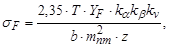
где 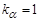; 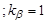- для материалов 1-й группы; 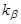=1,23,...,1,65 при изменении = 2,5...6,3

- для материалов 2-й группы; 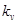- см. § 2.2, п.6

7. Провести сравнение :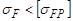

- если "нет", то вернуться к блоку 2 и выбрать новый материал;

- если "да", то перейти к следующему блоку.

8. Провести проверку передачи на изгибную прочность при дейст­вии максимальной нагрузкой (см. § 2.2, п. 23-25).

9. Определить основные размеры зубчатой пары:

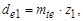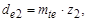а) внешние делительные диаметры: мм; мм.

б) угол головки зуба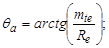

в) угол ножки зуба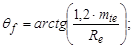

г) угол конуса вершин и впадин

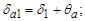
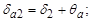
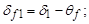
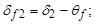
д) внешние диаметры вершин и впадин:

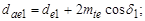
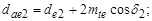
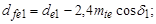
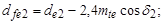
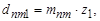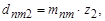е) диаметры в среднем сечении зуба: мм; мм.

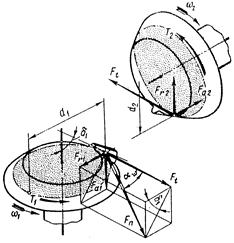
10. Определить силы в зацеплении (рис. 12):

а) окружная сила 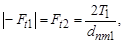Н.

б) осевая сила для шестерни(радиальная сила для колеса), где 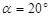- угол зацепления, 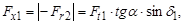Н;

в) радиальная сила для шестерни (осевая сила для колеса)

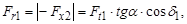Н.

Рис. 12. Схема сил в конической прямозубой передаче

2.3.2. Конструкция конических

зубчатых колес

Конические колеса изготавливают из круглого проката ( 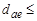120мм) ковкой и штамповкой ( 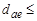500,…,700мм) (рис. 13).

Ориентировочные соотношения основных размеров конических ко­лес приведены ниже:

обод: толщина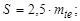

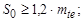
ширина ;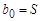

ступица: диаметр наружный 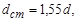где d - диаметр вала: толщина 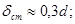- длина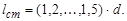

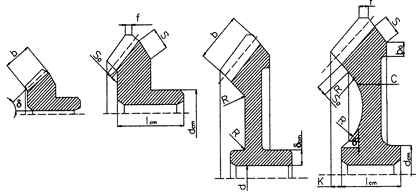
г) в) б) а)

Рис. 13. Конструкции конических зубчатых колес: а) круглый про­кат ( 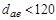мм); б) ковка ( 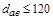мм); в) ковка ( 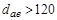мм);

г) штамповка ( 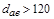мм)

диск: толщина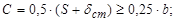

- радиусы закругления: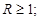

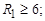
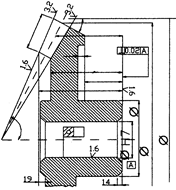Рис.14. Пример постановки размеров на чертеже конического зубчатого колеса

- штамповочный уклон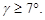

На торцах зубьев снимают фаски параллельно оси отверстия ко­леса 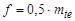с округлением до стандартного значения.

Для повышения точности изготовления так же, как и в цилиндри­ческих зубчатых передачах, в конических передачах нормируют погрешности размеров, формы и расположения базовых поверхностей заго­товок (рис. 14).

В таблице параметров (ГОСТ 2.403-75) на изображении конического зубчатого колеса должны быть указаны: средний нормальный модуль 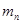; число зубьев 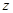; тип зуба; осевая форма зуба по ГОСТ 19325-73; средний угол наклона зуба 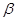; направление линии наклонa зуба; исходный контур со ссыл­кой на ГОСТ 16202-81; коэффициент смещения; угол делительного конуса 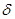, степень точности по ГОСТ 1758-81; межосевой угол передачи 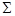; внешний окружной модуль 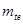; внешнее конусное расстоя­ние ; средний делитель­ный диаметр 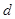; обозначе­ние чертежa сопряженного зубчатого колеса.

Погрешности изготов­ления деталей по осевым линейным размерам и по­грешности сборки приво­дят к неточному осевому положению в зубчатых конических передачах. Точность зацепления конических пар в проектируемых приводах достига­ют регулированием посредством осевого перемещения вала с закреплен­ной на нем шестерней.

2.4. Конструирование передачи "винт - гайка"

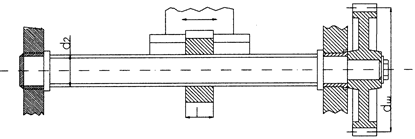
Передача "винт- гайка" (рис.15) служит для преобразования вращательного движения в поступательное. Кинематическое соотношение между линейной скоростью перемещения гайки 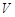и частотой вращения винта 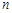определяется соотношением

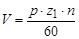, м/с,

где 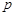- шаг винта, м; 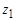- число заходов винта; 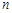- частота вращения винта, об/мин.

Рис.15. Передача "винт- гайка"

При простой и компактной конструкции передача "винт- гайка" позволяет получить большой выигрыш в силе или осуществлять точные перемещения. В соответствии с этим передачу "винт - гайка" приме­няют в механизмах, где необходимо создать большие усилия (домкра­ты, прессы), а также в механизмах точных перемещений (механизмы подачи станков, измерительные, установочные и регулировочные механизмы).