Тепловой и ветровой напоры воздуха

Для большинства зданий естественный воздухообмен является основным средством поддержания необходимых гигиенических условий в его помещениях. Природными силами, которые обусловливают движение воздуха в здании, являются гравитационное (тепловой напор) и ветровое (ветровой напор) давления.

Тепловой напор

Температура и плотность воздуха внутри и снаружи здания не постоянны, в связи с этим создаются разные давления по обеим сторонам ограждения. Удельный вес воздуха γ, Н/м³, как функция его температуры (t), может быть определен формулой

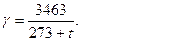(7.1)

Иллюстрация действия теплового напора представлена на рис. 7.1. На приведенной схеме поперечного разреза здания пол и потолок считаются условно воздухонепроницаемы, а стены по высоте (Н) не имеют проемов и одинаково однородны. Если воздух в помещении теплее наружного (t_в > t_н), согласно формулы (7.1) создается перепад давлений (γ_н - γ_в). По средине высоты располагается нейтральная зона, где этот перепад равен нулю, а максимальным значение 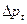, Па, будет в нижней и верхней частях стены. В нижней части холодный воздух проникает внутрь помещения (инфильтрация), а в верхней части (эксфильтрация) выходит из помещения. Максимальное значение перепада давлений вычисляется по формуле

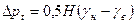. (7.2)

Для инженерных расчетов при закрытых нижних проемах принимается

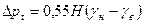. (7.2а)

Рис.7.1 – Схема действия теплового напора воздуха на здание

Ветровой напор

За счет действия ветра на наветренной стороне здания возникает повышенное статическое давление. На заветренной стороне статическое давление понижено. Таким образом, благодаря ветру на внешних поверхностях здания давление будет отличаться от давления внутри помещения. При анализе ветрового напора здание рассматривается отдельно стоящим, достаточно протяженным и длинной стороной перпендикулярным направлению ветра. В таком случае здание находится под максимальным воздействием ветра. Предполагается, что температуры внутреннего и наружного воздуха равны. Схемы эпюр положительного и отрицательного давления (которые также условно принимаются равномерными по высоте) приведены на рис. 7.2.

v p₁

k₁ p₂

k₂

Рис. 7.2 – Схема действия ветрового напора на здание

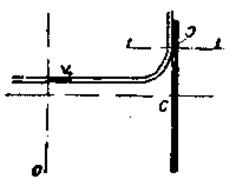
Для выяснения действия ветра на твердые тела необходимо знать распределение аэродинамических сил по поверхности тела. Установить основные закономерности позволит схема (см. рис. 7.3) взаимодействия пластины, расположенной перпендикулярно направлению воздушного потока. В потоке выделяется элементарная струйка [2].

Рис. 7.3 – Схема обтекания пластинки, перпендикулярной воздушному потоку

Для сечения О – О, взятого на достаточном расстоянии от пластинки и 1 – 1, когда струйка после поворота стала параллельной пластинке, можно записать уравнение Бернулли в виде

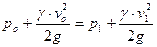, (7.3)

где р_о, р₁ – соответственно статические давления, Па, а v_o и v₁ - скорости в указанных сечениях; g – ускорение силы тяжести, м/с².

Формула (7.3) верна в предположении, что при повороте струйки потери отсутствуют. Если сечение О – О взято на достаточном расстоянии от пластинки, то v_o будет представлять скорость невозмущенного потока и р_о = р_а – атмосферное давление. Слагаемое 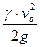представляет собой кинетическую энергию невозмущенного потока и по сути является скоростным напором.

Формулу (7.3) можно записать иначе

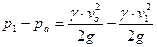или 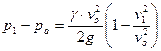. (7.4)

Левая часть уравнения является избыточным давлением, р_изб, в точке 1 по сравнению с атмосферным давлением р_а. Величина избыточного давления пропорциональна скоростному напору. Выражение в скобках представляет собой аэродинамический коэффициент, k, который показывает какая доля скоростного напора переходит в давление.

Тогда 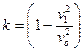. (7.5)

Аэродинамический коэффициент – безразмерная величина, не зависящая от системы единиц. Его величина может быть положительной (при v_o > v₁) и при v₁ = 0 принимает максимальное значение k = 1, указывающее на то, что вся кинетическая энергия переходит в давление. При v_o < v₁ аэродинамический коэффициент отрицателен – это означает, что давление на поверхности ниже атмосферного и в данной точке господствует разряжение. Поскольку кинетическая энергия всегда величина положительная, то знак избыточного давления зависит только от знака аэродинамического коэффициента.

В общем случае давление в любой точке находится следующим образом

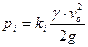. (7.6)

Следует заметить, что величина аэродинамического коэффициента определяется на основании модельного эксперимента в аэродинамических трубах и в конечном итоге зависит от шероховатости подстилающей поверхности, геометрии здания и направления ветра. При моделировании свободным поток считается либо на высоте верха здания, либо на уровне 100 м.

Для рассматриваемого на рис. 7.2 случая на наветренной стороне аэродинамический коэффициент принимается k₁ = 0,8, а для заветренной – k₂ = -0,4. Тогда по закону сохранения энергии давление внутри здания будет равно среднему между повышенным (р₁) на наветренной стороне и пониженным (р₂) на заветренной. Величина избыточного давления на стеновое ограждение определится следующим образом

. (7.7)

Если подставить в формулу (7.7) численные значения аэродинамических коэффициентов, то окончательно разность давлений за счет ветрового напора (индекс ‘о’ у величины v опущен) находится как

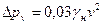. (7.8)

Ветровой напор можно уменьшить, если располагать здание в аэродинамической тени (защита другими зданиями или растительностью) или торцом к господствующим ветрам.

В инженерных расчетах принято, что гравитационное и ветровое давления действуют совместно. В холодный период года благодаря проникновению в помещение (инфильтрации) холодного воздуха происходят дополнительные теплопотери из-за необходимости подогрева холодного воздуха. Разность давлений воздуха на наружной и внутренней поверхностях ограждения, Δр, Па, в таком случае следует определять по формуле

Dр = 0,55 H (g_н - g_в) + 0,03g_нv², (7.9)