Необходимое условие устойчивости
Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде
D(p) = aopn + a1pn-1 + a2pn-2 + ... + an = ao(p-p1)(p-p2)...(p-pn) = 0,
где p1, p2, ..., pn - корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней
отрицательны, что можно записать какai = -|ai| < 0. Подставим их в уравнение:
a0 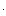 (p + |a1|)
(p + |a1|) 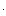 (p + |a2| - j
(p + |a2| - j  2)
2) 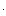 (p + |a2| + j
(p + |a2| + j  2)
2) 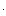 ... = 0.
... = 0.
Перемножая комплексно сопряженные выражения, получим:
a0 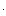 (p + |a1|)
(p + |a1|) 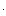 ((p + |a2|)2 + (
((p + |a2|)2 + (  2)2)
2)2) 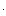 ... = 0.
... = 0.
После раскрытия скобок должно получиться выражение
a0 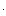 pn + a1
pn + a1 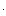 pn-1 + a2
pn-1 + a2 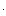 pn-2 + ... + an = 0.
pn-2 + ... + an = 0.
Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов a0,a1,...,an не будет отрицательным. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a0 > 0, a1 > 0, ... , an > 0. В дальнейшем будем рассматривать только уравнения, где a0 > 0. В противном случае уравнение домножается на -1.
Рассмотренное условие является необходиным, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.
Дата добавления: 2015-07-24; просмотров: 626;
