Применение математического моделирования для организации перевозки заданных грузопотоков в условиях отсутствия единого базового порта
Представляемая задача рассматривает случай эксплуатационной практики в более общем (в сравнении с изложенным выше) виде – перевозку разных грузов между разными (достаточно многочисленными) портами в рамках долгосрочного контракта (не менее 3 месяцев) без привязки к единому базовому порту. Отличительная особенность – работа разнотипного флота на нескольких схемах движения (которые могут не иметь пунктов пересечения). Цель задачи – установление необходимого количества судов каждого типа и закрепление их за определенными (в ходе решения) схемами движения во исполнение плановых обязательств с максимальной эффективностью. Иными словами – выявление необходимых ресурсов флота и их рациональное использование. Эти управленческие вопросы во всей полноте либо в частностях (например, в пределах одного рейса, перевозка одного груза и т.п.) присущи работе судов и в трампе и в линейном плавании. Так, практика вполне успешного функционирования линейной компании, перевозящей контейнеры по Европе (до 30-ти портов захода) показала, что при хаотичном (т.е. без заведомо установленных схем) движении флота при всем его многочисленном составе компания теряет в месяц от 6-ти до 8-ми отходов, которые она, будучи не в состоянии осуществить, вынуждена передавать другим линиям. В то же время при правильно определенных маршрутах следования судов (как будет показано ниже) возможность таких ситуаций исключается.
Задачи эффективной организации перевозок неоднократно находили отражение в разных математических моделях. Путь развития, от использования классической транспортной задачи при оптимизации схем движения тоннажа для транспортно-однородных грузов (впервые введенной в практику работы Черноморского пароходства), включает и многошаговую модель линейного судоходства, позволяющую одновременно выбирать схему обхода портов и определять объемы перевозок как основных, так и дополнительно привлекаемых грузов. Аппарат для решения подобных моделей – линейное программирование сначала только с непрерывными переменными, а с появлением быстродействующих электронных машин и с целочисленными и частично целочисленными переменными.
Однако, практическая реализация этих моделей встречает немалые затруднения. Прежде всего, это касается последней из названных моделей, которая прошла только лабораторную апробацию. Большая размерность этой задачи, при необходимости создающей «кольцевые» маршруты, связана со столь же большим объемом подготовительной работы по вводу информации. Это снижает практическую значимость модели при несомненных теоретических достоинствах. Создание специальных программ для автоматизации ввода могло бы приблизить данную модель к использованию при организации перевозок.
Наиболее широко известна в практике управления работой флота в трампе задача, вошедшая в литературу как «расстановочная» в нескольких модификациях. Она характеризуется упрощенностью изложения, заключающейся в решении при так называемом предположении «существования», а именно, схемы движения в такой задаче считаются известными заранее. Действительно, если схемы определены верно, то это существенно сокращает трудоемкость поиска решения.
Такая модель, охватывающая достаточно широкий спектр практических задач, все-таки является частным случаем, поскольку ориентирована скорее на направления перевозок, чем на схемы движения в общем смысле. Иными словами, из постановки «расстановочной» задачи исключен тот факт, что различные схемы движения, включающие более двух портов, могут содержать одинаковые составные части. В то же время учет этого предоставил бы алгоритму возможность «перебрасывать» груз со схемы на схему в целях наиболее полного использования грузоподъемности судов, тем самым в конечном счете обеспечивая сокращение издержек. При использовании для решения пакета прикладных программ с непрерывными переменными сформулированное выше обстоятельство может быть реализовано вручную при округлении результатов до целых чисел (означающих количество рейсов). Процесс округления, проведенный правильно в рамках ограничений задачи и направленный на рациональное использование материальных ресурсов – провозной способности флота, в ряде случаев достаточно сложен.
Решение той же задачи с применением пакета прикладных программ с целочисленными переменными избавляет пользователя от необходимости округления. Но результаты оставляют желать лучшего, т.к. округление дробных величин в большую сторону влечет фактически «недогруз» рейсов, а с ним и большее количество судов а, следовательно, и затрат.
Для устранения указанного недостатка разработана новая модификация «расстановочной» модели с двумя типами переменных – целочисленными и непрерывными. Сочетание этих переменных позволяет избежать несовместности ограничений при округлении. Модель основывается на предварительно определенных оптимальных (по критерию минимума балластных пробегов) схемах движения тоннажа.
Целочисленные переменные xijk обозначают количество рейсов i-го типа судна на j-той схеме с k-тым грузом.
Непрерывные переменные yijk – количество недовезенного k-го груза i-тым типом судна на j-той схеме. Формализация модели имеет вид:
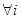 :
: 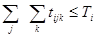 ,
,
где Тi [18] – бюджет времени работы i-го типа судна;
tijk – продолжительность участка рейса i-го типа судна на j-ой схеме с k-ым грузом.
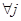 :
: 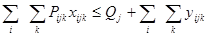 ,
,
где Qj – количество груза, которое должно быть перевезено по схеме j.
Это ограничение позволяет перевозить по схеме количество груза не строго равное заданному объему по схеме движения, вплоть до полного расформирования схемы.
3а) 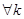 :
:  ,
,
3б) 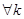 :
: 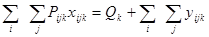 ,
,
где Qk – количество заявленного к перевозке k-го груза.
Ограничение (3а) предполагает возможность перевозки k-го груза не в полном объеме (с малым отклонением), если по расчету окажется выгоднее не довезти груз, чем посылать в рейс недостаточно загруженное судно.
Ограничение (3б) не допускает такой возможности, т.е. груз будет перевезен полностью. При этом допускает недогруженность судна. Выбор типа ограничения зависит от конкретной эксплуатационной ситуации.
4) 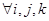 :
: 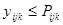 .
.
5) 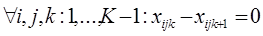 .
.
Это ограничение объединяет в один рейс перевозки разных грузов по данной схеме. Любое 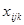 соответствует количеству рейсов судна типа i на схеме j.
соответствует количеству рейсов судна типа i на схеме j.
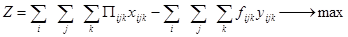 ,
,
где 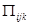 - прибыль за рейс от перевозки k-го груза i-ым типом судна по схеме j,
- прибыль за рейс от перевозки k-го груза i-ым типом судна по схеме j,
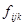 - прибыль от перевозки 1 т k-го груза i-ым типом судна по схеме j.
- прибыль от перевозки 1 т k-го груза i-ым типом судна по схеме j.
Целевая функция носит условный характер, т.к. включает в себя упущенную прибыль вследствие недовоза груза, однако сопоставимые показатели эффективности целевой функции и ограничения модели направляют алгоритм на максимально возможное заполнение судов, допуская перераспределение груза между схемами вплоть до полного расформирования отдельных неэффективных первичных схем.
Таким образом, математическое моделирование при организации перевозки заданного грузопотока представляется целесообразным осуществлять поэтапно, начиная с построения «отправных» маршрутов применительно к «усредненному» судну (как это было принято ранее) и далее следуя упомянутой выше модели, позволяющей наилучшим образом использовать конкретные поименованные суда для получения максимальной прибыли от перевозок.
Применение этой модели, имея целью достижение вышеозначенного результата, предусматривает также и предоставление наибольших удобств для пользователя, устраняя необходимость дополнительной доработки решения. Процедура ввода информации не затруднительна и, кроме того, весьма просто алгоритмизируется в компьютерную программу, что в свою очередь может способствовать повышению эффективности предлагаемого метода.
Однако, при подготовке специалистов-управленцев представляется весьма полезной именно доработка решения в части округления результатов после применения модели линейного программирования с непрерывными переменами. В ходе этой процедуры учащиеся могут реализовать знания, полученные в процессе учебы, а также на конкретном примере получить практический навык рационального использования ресурсов флота. Ниже излагаются основные этапы математического моделирования организации перевозки грузопотоков – оптимизация схем движения тоннажа и расстановки флота по схемам на базе модели линейного программирования с непрерывными переменными. Результаты обеих этих задач могут быть расценены как «стратегия» при принятии управленческого решения на перспективу (например, квартал).
Организация схем движения тоннажа производится по критерию «минимум тоннаже-миль в балласте». Исходными данными для задачи являются грузопотоки и типы судов, подобранные соответственно свойствам грузов и навигационным условиям. Прежде всего, исходные грузопотоки легких грузов обращаются в тоннаже-потоки (D) по известной формуле: 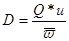 , где Q – количество грузов в тоннах, u – удельный погрузочный объем,
, где Q – количество грузов в тоннах, u – удельный погрузочный объем, 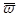 - средняя (по судам) удельная грузовместимость.
- средняя (по судам) удельная грузовместимость.
Далее выявляются порты-источники и порты-потребители тоннажа в балласте. Для этого строится таблица-шахматка, в которой по горизонтали и по вертикали перечисляются все порты. Все данные по отправкам тоннажа заносятся в таблицу. Правый крайний столбец таблицы включает сумму всего отправляемого тоннажа, нижняя строка – сумму прибывающего. По каждому порту из значения строки прибытия вычитается значение столбца отправления, результат со знаком «+» означает излишек тоннажа, со знаком «-» - недостаток. Эти значения располагаются на диагонали таблицы. Очевидно, что излишки тоннажа следует вывезти в те порты, где наблюдается нехватка. Возникает классическая транспортная задача распределения ресурсов по потребностям, в качестве показателей эффективности которой выступают расстояния между портами:
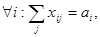 ai -ресурс i-го порта;
ai -ресурс i-го порта;
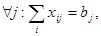 bi -потребность j-го порта;
bi -потребность j-го порта;
 - количество тоннажа в балласте, перевозимое из порта i на порт j.
- количество тоннажа в балласте, перевозимое из порта i на порт j.
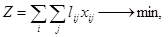 где lij – расстояние между портами.
где lij – расстояние между портами.
Задача может быть решена с применением пакета прикладных программ LPX или любым известным методом вручную.
 Результаты решения вносятся в таблицу. С этого момента таблица включает всю информацию о перевозках тоннажа в грузу или балласте, исходя из которой составляются схемы движения круговых рейсов. По каждой схеме (на всех ее участках) перевозится одно и то же количество тоннажа, но количество груза в тоннах может быть разным вследствие отличия в величине удельного погрузочного объема. Начинать построение схем удобнее всего с наименьшего значения тоннажа в балласте (далее следовать по их возрастанию). Например, из порта 3 на порт 1 перевозится Dт (самое маленькое значение тоннажа в балласте). Эта перевозка составит начальный участок схемы: 3 в балласте 1.
Результаты решения вносятся в таблицу. С этого момента таблица включает всю информацию о перевозках тоннажа в грузу или балласте, исходя из которой составляются схемы движения круговых рейсов. По каждой схеме (на всех ее участках) перевозится одно и то же количество тоннажа, но количество груза в тоннах может быть разным вследствие отличия в величине удельного погрузочного объема. Начинать построение схем удобнее всего с наименьшего значения тоннажа в балласте (далее следовать по их возрастанию). Например, из порта 3 на порт 1 перевозится Dт (самое маленькое значение тоннажа в балласте). Эта перевозка составит начальный участок схемы: 3 в балласте 1.
D


 Просматриваются перевозки груза из порта 1, избирается перевозка, допустим на порт 4, она становится следующим участком схемы: 3 в балласте 1 в грузу Q1 4 в грузу Q2 …
Просматриваются перевозки груза из порта 1, избирается перевозка, допустим на порт 4, она становится следующим участком схемы: 3 в балласте 1 в грузу Q1 4 в грузу Q2 …
D D D
и т.д. до возвращения в исходный порт 3. В итоге по сумме схем должны быть полностью[19] перевезены все грузы и тоннаж в балласте.
Следующий этап - расстановка флота по схемам движения.
Параметром управления xij целесообразно считать количество рейсов судов i-го типа, выполняющих перевозки на j-ой схеме.
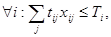 где tij -время рейса i-го типа судна на j-ой схеме, Тi – бюджет времени i-го типа судна.
где tij -время рейса i-го типа судна на j-ой схеме, Тi – бюджет времени i-го типа судна.
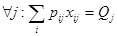 , где Qj - количество груза, которое должно быть перевезено по j-той схеме; Pij – загрузка i-го типа судна j-ым грузом.
, где Qj - количество груза, которое должно быть перевезено по j-той схеме; Pij – загрузка i-го типа судна j-ым грузом.
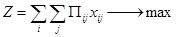 , где Пij - прибыль от работы i-го типа судна на j-той схеме за 1 рейс, рассчитывается как разность между доходами от перевозки грузов и расходами по эксплуатации судна и заходам в порты.
, где Пij - прибыль от работы i-го типа судна на j-той схеме за 1 рейс, рассчитывается как разность между доходами от перевозки грузов и расходами по эксплуатации судна и заходам в порты.
Для решения задачи может быть применен пакет прикладных программ LPX. Полученное оптимальное решение составит набор переменных и их значений, представляющих собой количество рейсов, которые должны выполнить суда i-го типа на схеме j. Эти значения могут оказаться дробными числами и подлежат округлению, что составляет предмет доработки решения. При округлении, проводимом в пределах ограничений по бюджету времени, вполне возможно осуществлять переброску груза с одной схемы на другую (если отдельные участки схем совпадают), а также с судна на судно, например, с большего на меньшее, если по прибыли окажется выгоднее полностью использовать грузоподъемность последнего, чем направлять в очередной рейс недогруженное большое судно. Может наблюдаться и обратная ситуация – полная загрузка большего судна за счет меньшего. В результате округления некоторые схемы движения могут быть полностью устранены. Причина этого в том, что первичные схемы движения составляются для «усредненного» судна и могут быть расценены как некая «заготовка» для последующих вычислений. Конечно, в большей мере эта «заготовка» сохраняется неизменной при расстановке флота. В отдельных случаях может быть сформирована дополнительная схема для довозки (на 1 рейс) небольшой части груза и предложено привлечение нового судна (ранее не участвующего в расчетах), наиболее подходящего для этой цели. Таким образом, имеет место последовательное улучшение процесса. Окончательный оптимальный вариант расстановки флота определяется в результате округления и состоит из целочисленных значений количества рейсов каждого судна типа i на схеме j. Следующий этап организации перевозки заданных грузопотоков не требует математического моделирования. Он заключается во вводе флота в график работы на ближайший месяц и представляет собой «тактику» управления для выполнения уточненной заявки на перевозку грузов. На этом шагу и устанавливается количество судов, необходимое для своевременного (в пределах месяца) осуществления отгрузки.
В заключение следует еще раз подчеркнуть, что решение такой достаточно крупной и сложной задачи не может быть реализовано в рамках единой модели. Поэтому предлагается комплексное использование поэтапной[20] оптимизации на основе уточняющейся информации приближающейся временной перспективы в части грузопотоков и местонахождения судов.
Дата добавления: 2015-07-24; просмотров: 1493;
