МЕХАНИЧЕСКИЕ СВОЙСТВА

11.1. Деформация. Способы деформирования

Механическое воздействие на тело изменяет взаимное распо­ложение его частиц. Деформация — изменение взаимного рас­положения точек тела, приводящее к изменению его формы и раз­меров.

При действии на тело внешней деформирующей силы расстоя­ние между частицами меняется. Это приводит к возникновению внутренних сил, стремящихся вернуть атомы (ионы) в перво­начальное положение. Мерой этих сил является механическое на­пряжение. Непосредственно напряжение не измеряется. В ряде случаев его можно вычислить через внешние силы, действующие на тело.

В зависимости от условий внешнего воздействия различают не­сколько способов деформирования, которые рассматриваются ниже.

Растяжение (сжатие)

К стержню (бруску) длиной / и площадью поперечного сечения S прикладывается сила F, направленная перпендикулярно сечению (рис. 11.1).В результате этого в теле возникает меха­ническое напряжение а, которое в данном случае характеризу­ется отношением силы к площади поперечного сечения стержня (малое изменение площади поперечного сечения не учитывается):

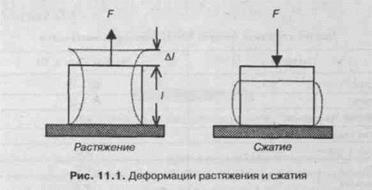
Под действием приложенной силы длина стержня изменяется на некоторую величину Л/, которая называется абсолютной деформа­цией. Величина абсолютной деформации зависит от первоначальной длины стержня, поэтому степень деформации выражают через отно­шение абсолютной деформации к первоначальной длине. Это отно­шение называется относительной деформацией (е):

где Е — модуль Юнга, Па (модуль продольной упругости).

При упругой деформации напряжение прямо пропорциональ­но величине деформации.

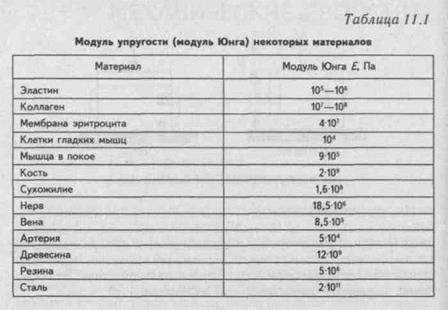
Модуль Юнга численно равен напряжению, увеличивающему длину образца в два раза (практически разрушение образцов на­ступает при значительно меньших напряжениях). В табл. 11.1 пред­ставлены значения модулей упругости некоторых материалов.

В большинстве случаев при растяжении или сжатии степень деформации в различных сечениях стержня различна. Это можно

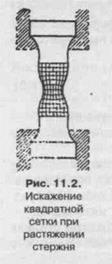
увидеть, если на поверхность тела нанести квадратную сетку. По­сле деформирования сетка исказится. По характеру и величине этого искажения можно судить о распределении напряжения вдоль образца (рис. 11.2).

Видно, что изменения формы ячеек сетки мак­симальны в средней части стержня и почти от­сутствуют на его краях.

Сдвиг

Деформация сдвига возникает, если на тело дей­ствует касательная сила, приложенная параллель­но закрепленному основанию (рис. 11.3). В этом слу­чае направление смещения свободного основания параллельно приложенной силе и перпендикуляр­но боковой грани. В результате деформации сдвига прямоугольный параллелепипед превращается в ко­соугольный. При этом боковые грани смещаются на некоторый угол у, называемый углом сдвига.

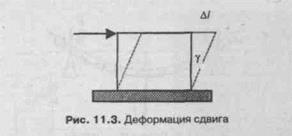
Абсолютная деформация сдвига измеряется величиной смеще­ния свободного основания (Д/). Относительная деформация сдви­га определяется через тангенс угла сдвига tgy, называемый отно­сительным сдвигом. Так как угол у обычно мал, то можно считать

tg(y) - У-

При сдвиге в образце возникает напряжение сдвига х (касатель­ное напряжение), которое равно отношению силы (F) к площади основания (S), параллельно которому действует сила:

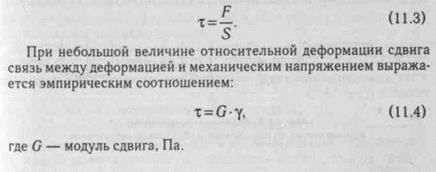
Изгиб

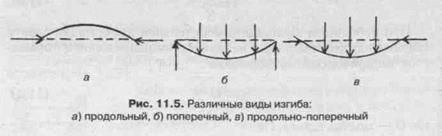
Этот вид деформации характеризуется искривлением оси или срединной поверхности деформируемого объекта (балка, стер­жень) под действием внешних сил (рис. 11.4). При изгибе один наружный слой стержня сжимается, а другой наружный слой рас­тягивается. Средний слой (называемый нейтральным) изменяет лишь свою форму, сохраняя длину. Степень деформирования бру­ска, имеющего две точки опоры, определяется по перемещению X, которое получает середина стержня. Величина X называется стре­лой прогиба.

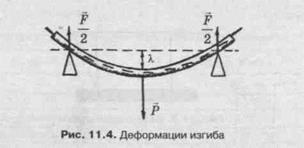
Применительно к прямому брусу в зависимости от направле­ния действующих сил изгиб называют продольным или попе­речным. Продольный изгиб возникает под действием сил, направ­ленных вдоль бруса и приложенных к его концам навстречу друг другу (рис. 11.5, а). Поперечный изгиб возникает под действием сил, направленных перпендикулярно брусу и приложенных как к его концам, так и в средней части (рис. 11.5, б). Встречается так­же и смешанный продольно-поперечный изгиб (рис. 11.5, в).