Нормальное распределение. Когда большое количество данных собирают, представляют в табличном виде и отображают в виде гистограммы или огибающей
Когда большое количество данных собирают, представляют в табличном виде и отображают в виде гистограммы или огибающей, они часто образуют колоколообразное симметричное распределение, известное как нормальное распределение. Большинство его элементов располагаются вблизи среднего (верхняя точка колокола), и этот колокол резко спадает у самой большой и у самой малой величины. Такая форма кривой представляет особый интерес, поскольку она возникает и тогда, когда результат процесса основан на множестве случайных событий, все из которых происходят независимо. Демонстрационное устройство, показанное на рис. П4, позволяет увидеть, как из случайных событий складывается нормальное распределение. Случайный фактор — упадет ли стальной шарик влево или вправо каждый раз, когда он попадает в развилку, — приводит к симметричному распределению: больше шариков падают прямо посередине, но время от времени один из них достигает одного из крайних отделений. Это удобная визуализация того, что имеется в виду под случайным распределением, близким к нормальному распределению.

Рис. П4. Устройство для демонстрации нормального распределения случайной величины.Устройство держат вверх ногами, пока все стальные шарики не скатятся в резервуар. Затем устройство переворачивают и держат вертикально, пока шарики, пройдя по полю со штырьками, не скатятся в 9 колонок-выемок внизу. Точное количество шариков, попавших в каждую колонку, в разных демонстрациях будет неодинаковым. Однако в среднем высота колонок из шариков будет примерно повторять нормальное распределение, когда самая высокая колонка будет в центре, а высоты остальных колонок будут снижаться в направлении к краям.
Нормальное распределение (рис. П5) — это математическое представление идеализованного распределения, приближенно создаваемого устройством, показанным на рис. П4. Нормальное распределение показывает вероятность того, что элементы в группе с нормальным распределением будут отличаться от среднего на любую заданную величину. В процентах на рис. П5 показана доля площади, лежащей под кривой между указанными величинами шкалы; общая площадь под кривой соответствует группе в целом. Примерно две трети всех случаев (68%) попадают в интервал между плюс и минус одним стандартным отклонением от среднего (±1σ); 95% всех случаев — в интервал ±2σ; и практически все случаи (99,7%) — в ±3σ.
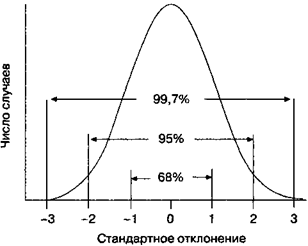
Рис. П5. Нормальное распределение.Кривую нормального распределения можно построить, используя стандартное отклонение и среднее. Площадью под кривой, лежащей левее -3σ и правее +3σ, можно пренебречь.
Более подробный список площадей под частями кривой нормального распределения приведен в табл. П4.
Таблица П4. Площадь участков под кривой нормального распределения как часть общей площади под ней
| Стандартное отклонение | (1) Площадь левого участка от данного значения | (2) Площадь правого участка от данного значения | (3) Площадь участка между данным значением и средней |
| -3,0 σ | 0,001 | 0,999 | 0,499 |
| -2,5 σ | 0,006 | 0,994 | 0,497 |
| -2,0 σ | 0,023 | 0,977 | 0,477 |
| -1,5 σ | 0,067 | 0,933 | 0,433 |
| -1,0 σ | 0,159 | 0,841 | 0,341 |
| -0,5 σ | 0,309 | 0,691 | 0,191 |
| 0,0 σ | 0,500 | 0,500 | 0,000 |
| +0,5 σ | 0,691 | 0,309 | 0,191 |
| +1,0 σ | 0,841 | 0,159 | 0,341 |
| +1,5 σ | 0,933 | 0,067 | 0,433 |
| +2,0 σ | 0,977 | 0,023 | 0,477 |
| +2,5 σ | 0,994 | 0,006 | 0,494 |
| +3,0 σ | 0,999 | 0,001 | 0,499 |
Давайте при помощи табл. П4 проследим, как получаются величины 68% и 95%, показанные на рис. П5. В табл. П4 в третьей колонке находим, что между -1σ и средним лежит 0,341 общей площади и между +1σ и средним тоже 0,341 общей площади. В сумме эти величины дают 0,682, что на рис. П5 показано как 68%. Сходным образом площадь от -2σ до +2σ составит 2 х 0,477 = 0,954, показанные как 95%.
Дата добавления: 2015-07-22; просмотров: 1001;
