Значимость различия
Во многих психологических экспериментах данные собираются по двум группам испытуемых; одна группа подвергается специфическим экспериментальным воздействиям, а другая служит контрольной. Вопрос в том, существует ли различие между средними показателями этих групп, и если есть, то выдерживается ли оно для всей группы, из которой были взяты эти две выборки. Проще говоря, отражает ли различие между двумя группами истинное различие или оно возникло вследствие ошибки выборки.
В качестве примера сравним показатели экзамена по чтению у выборки мальчиков-первоклассников с показателями у выборки девочек-первоклассниц. Что касается средних показателей, то они у мальчиков ниже, но здесь есть значительное перекрытие; некоторые мальчики справляются исключительно хорошо, а некоторые девочки — крайне плохо. Поэтому мы не можем принять это различие средних, не проведя тест на статистическую значимость. Только тогда можно будет решить, отражают ли наблюдаемые различия в выборке истинные различия в группе или же они объясняются ошибкой выборки. Если некоторые более одаренные девочки и некоторые более тупые мальчики оказались выбраны по чистой случайности, то различие можно объяснить ошибкой выборки.
В качестве еще одного примера предположим, что мы провели эксперимент по сравнению крепости рукопожатия у мужчин правшей и левшей. В верхней части табл. П5 показаны гипотетические данные такого эксперимента. Выборка из 5 мужчин-правшей в среднем на 8 кг сильнее выборки из 5 мужчин левшей. Что вообще можно вывести из таких данных о мужчинах левшах и правшах? Можно ли утверждать, что правши сильнее? Очевидно, нет, поскольку среднее, полученное у большинства правшей, не отличалось бы от среднего у большинства левшей; один примечательно отличающийся показатель величиной 100 говорит о том, что мы имеем дело с неопределенной ситуацией.
Таблица П5. Значимость различия
Пример 1
| Сила сжатия в килограммах, Мужчина-правша | Сила сжатия в килограммах, Мужчина-левша |
| Сумма 290 | Сумма 250 |
| Среднее 58 | Среднее 50 |
Пример 2
| Сила сжатия в килограммах, Мужчина-правша | Сила сжатия в килограммах, Мужчина-левша |
| Сумма 290 | Сумма 250 |
| Среднее 58 | Среднее 50 |
Два примера, показывающих различие между средними. Разница средних одинакова (8 кг) в верхней и нижней части таблицы. Однако, данные нижней части указывают на более надежное различие средних, чем данные в верхней части таблицы.
Теперь предположим, что в результате эксперимента получены результаты, показанные в нижней части той же табл. П5. Мы снова видим то же самое различие средних, равное 8 кг, но теперь эти данные вызывают большее доверие, поскольку показатели у левшей получились систематически ниже, чем у правшей. Статистика позволяет очень точно учесть надежность различий среднего, так чтобы при определении, какое из двух различий более надежно, не зависеть только от интуиции.
Эти примеры показывают, что значимость полученного различия зависит и от его величины, и от варьируемости сравниваемых средних. Зная стандартную ошибку среднего, можно вычислить стандартную ошибку различия между двумя средними σDM. Затем можно оценить полученное различие при помощи критического отношения — отношения полученной разницы средних (DM) к стандартной ошибке различия между средними:
Критическое отношение = 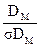
Это отношение позволяет оценить значимость различия между двумя средними. Как простейшее правило, критическое отношение должно быть не менее 2,0, чтобы разница средних считалась значимой. Во всей этой книге выражение о «статистической значимости» разницы средних означает, что критическое отношение у них не меньше такого.
Почему в качестве статистически значимого выбрано критическое отношение, равное 2.0? Просто потому, что такая или большая величина может выпасть случайно только в 5% случаев. Откуда взялись эти 5%? Критическое отношение можно считать стандартным показателем, поскольку это просто разница двух средних, выраженная в числе стандартных ошибок. Обращаясь ко 2-й колонке табл. П4, замечаем, что вероятность того, что стандартное отклонение составляет 2,0 при случайном совпадении, равна 0,023. Поскольку вероятность отклонения в противоположную сторону тоже равна 0,023, общая вероятность составит 0,046. Это означает что когда средние групп одинаковы, критическое отношение может случайно оказаться равным 2,0 (или более) в 46 случаях из 1000, или в 5% случаев.
Элементарное правило, говорящее, что критическое отношение должно быть не менее 2,0, именно таково — это произвольное, но удобное правило, задающее 5%-ный уровень значимости. Следуя этому правилу, вероятность ошибочного решения о том, что разница средних существует, тогда как на самом деле это не так, будет меньше 5%. Не обязательно пользоваться 5%-ным уровнем; в некоторых экспериментах может потребоваться более высокая значимость, в зависимости от того, насколько допустима ошибка заключения.
Пример вычисления критического отношения.Для вычисление критического отношения надо определить стандартную ошибку разницы двух средних по следующей формуле:
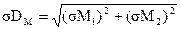
В этой формуле σМ1 и σМ2 — стандартные ошибки двух сравниваемых средних.
В качестве иллюстрации предположим, что нам надо сравнить достижения первоклассников — мальчиков и девочек на экзамене по чтению в США. Берется случайная выборка мальчиков и девочек и подвергается тестированию. Предположим, что средний показатель у мальчиков равен 70 при стандартной ошибке среднего 0,40, а средний показатель у девочек — 72 при стандартной ошибке среднего 0,30. На основе этих выборок надо решить, есть ли это реальное различие между успехами мальчиков и девочек в чтении в группе в целом, Данные выборки показывают, что оценки у девочек больше, чем у мальчиков, но можно ли заключить, что мы получили бы то же самое, протестировав всех первоклассников США? Решить это позволяет критическое отношение.
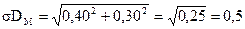
Критическое отношение = 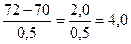
Поскольку критическое отношение значительно выше 2,0, можно утверждать, что наблюдаемое среднее различие статистически значимо на 5%-ном уровне. Поэтому можно заключить, что между мальчиками и девочками существует надежное различие в успехах по чтению. Заметьте, что критическое отношение может быть положительным и отрицательным, в зависимости от того, какое среднее из какого вычитается; при интерпретации критического отношения учитывается только его величина, но не знак.
Дата добавления: 2015-07-22; просмотров: 2871;
