Насколько репрезентативно среднее?
Насколько хорошо среднее выборки отражает среднее всей группы? Если измерять рост у случайной выборки из 100 студентов колледжа, насколько хорошо среднее этой выборки предсказывает истинное среднее группы (то есть средний рост всех студентов колледжа)? Это все вопросы, связанные с выводом о группе на основе данных выборки.
Точность такого вывода зависит от ошибок выборки. Предположим, мы сделали две случайных выборки из одной и той же группы и для каждой из них подсчитали среднее. Какого различия между одним и другим средним можно ожидать в результате случая?
Последующие случайные выборки из той же группы будут давать разные средние, образуя распределение выборки средних вокруг истинного среднего данной группы. Эти выборки средних сами по себе являются величинами, для которых можно подсчитать стандартное отклонение. Это стандартное отклонение называется стандартной ошибкой среднего; оно обозначается sM и вычисляется по следующей формуле:
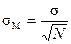
где σ — стандартное отклонение выборки, а N — количество случаев, по которым вычисляется каждое среднее.
Согласно этой формуле, величина стандартной ошибки среднего уменьшается с увеличением величины выборки; поэтому среднее, основанное на более крупной выборке, является более достоверным (оно скорее окажется ближе к истинному среднему всей группы). Этого можно было ожидать и на основе здравого смысла. Стандартная ошибка среднего ясно показывает, насколько неопределенно полученное среднее. Чем больше объем выборки, тем меньше неопределенность среднего.
Дата добавления: 2015-07-22; просмотров: 873;
