Перевод целых чисел из одной системы счисления в другую
Поскольку одно и то же число может быть записано в различных системах счисления, встает вопрос о переводе представления числа из одной системы (p) в другую (q) – будем обозначать такое преобразование Zp 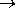 Zq.
Zq.
Теоретически возможно произвести его при любых q и p.
Однако подобный прямой перевод будет затруднен тем, что придется выполнять операции по правилам арифметики недесятичных систем счисления.
По этой причине более удобными с практической точки зрения оказываются варианты преобразования с промежуточным переводом Zp 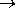 Zr
Zr 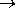 Zq с основанием r, для которого арифметические операции выполнить легко.
Zq с основанием r, для которого арифметические операции выполнить легко.
Такими удобными основаниями являются r = 1 и r = 10, т.е. перевод осуществляется через унарную или десятичную систему счисления.
8.3. Преобразование Zp 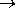 Z1
Z1  Zq
Zq
Идея алгоритма перевода предельно проста:
1. положим начальное значение Zq := 0;
2. из числа Zp вычтем 1 по правилам вычитания системы p, т.е. Zp := Zp–1 и добавим ее к Zq по правилам сложения системы q, т.е. Zq := Zq + 1;
3. будем повторять эту последовательность действий, пока не достигнем Zp = 0.
Правила сложения с 1 и вычитания 1 могут быть записаны следующим образом:
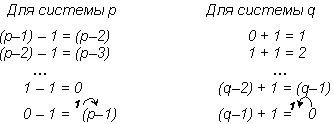
Промежуточный переход к унарной системе счисления в данном случае осуществляется неявно – используется упоминавшееся выше свойство независимости значения числа от формы его представления. Рассмотренный алгоритм перевода может быть легко реализован программным путем.
Пример 1. Выполнить преобразование 223  Z6. Последовательность действий и промежуточные результаты для наглядности представим в виде таблицы:
Z6. Последовательность действий и промежуточные результаты для наглядности представим в виде таблицы:
| Шаг | |||||||||
| Z3 - 1 | |||||||||
| Z6 + 1 |
Следовательно, 223 = 126.
8.4. Преобразование Zp  Z10
Z10 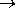 Zq
Zq
Очевидно, первая и вторая часть преобразования не связаны друг с другом, что дает основание рассматривать их по отдельности.
Алгоритмы перевода Z10 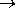 Zq
Zq
Многочлен (1) для Zq может быть представлен таким образом:
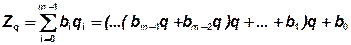 (2)
(2)
где m – число разрядов в записи Zq, а bj (j = 0...m–1) – цифры числа Zq.
Разделим число Zq на две части по разряду номер i;
Число, включающее m–i разрядов с m–1-го по i-й обозначим 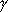 i,
i,
а число с i разрядами с i–1-го по 0-ой – 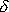 i.
i.
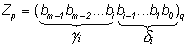 |
Очевидно, i
 [0,m–1],
[0,m–1], 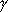 0 =
0 = 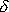 m-1 = Zq.
m-1 = Zq.
Позаимствуем из языка PASCAL обозначение двух операций:
· div – результат целочисленного деления двух целых чисел
· mod – остаток от целочисленного деления.
Например:
13 div 4=3;
13 mod 4 = 1.
Теперь если принять 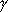 m-1 = bm-1, то в (2) усматривается следующее рекуррентное соотношение:
m-1 = bm-1, то в (2) усматривается следующее рекуррентное соотношение:
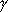 i =
i = 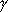 i+1 · q + bi,
i+1 · q + bi,
из которого, в свою очередь, получаются выражения:
 (3)
(3)
Аналогично, если принять 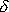 0 = b0, то для правой части числа будет справедливо другое рекуррентное соотношение:
0 = b0, то для правой части числа будет справедливо другое рекуррентное соотношение:
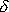 i =
i = 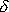 i-1 + bi ·qi,
i-1 + bi ·qi,
из которого следуют:
 (4)
(4)
Из соотношений (3) и (4) непосредственно вытекают два способа перевода целых чисел из 10-й системы счисления в систему с произвольным основанием q.
Способ 1 является следствием соотношений (3), из которых просматривается следующий алгоритм перевода.
1. Целочисленно разделить исходное число (Z10) на основание новой системы счисления (q) и найти остаток от деления – это будет цифра 0-го разряда числа Zq.
2. Частное от деления снова целочисленно разделить на q с выделением остатка; процедуру продолжать до тех пор, пока частное от деления не окажется меньше q.
3. Образовавшиеся остатки от деления, поставленные в порядке, обратном порядку их получения, и представляют Zq.
Обычно процесс первода представляют в виде "лестницы".
Пример 2. Выполнить преобразование 12310 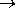 Z5.
Z5.
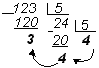
Остатки от деления (3,4) и результат последнего целочисленного деления (4) образуют обратный порядок цифр нового числа. Следовательно, 12310 = 4435.
Полученное число нельзя читать "четыреста сорок три", поскольку десятки, сотни, тысячи и прочие подобные обозначения чисел относятся только к десятичной системе счисления.
Читать число следует простым перечислением его цифр с указанием системы счисления ("число четыре, четыре, три в пятеричной системе счисления").
Способ 2 вытекает из соотношения (4); действия производятся в соответствии со следующим алгоритмом:
1. Определить m–1 – максимальный показатель степени в представления числа по форме (1) для основания q.
2. Целочисленно разделить исходное число (Z10) на основание новой системы счисления в степени m – 1 (т.е. qm-1) и найти остаток от деления. Результат деления определит первую цифру числа Zq;
3. Остаток от деления целочисленно разделить на qm-2, результат деления принять за вторую цифру нового числа; найти остаток;
4. Продолжать эту последовательность действий, пока показатель степени q не достигнет значения 0.
Продемонстрируем действие алгоритма на том же примере, что был рассмотрен выше. Определить m–1 можно либо путем подбора
(50=1<123; 51=5<123; 52=25<123; 53=125>123, следовательно, m–1=2),
либо логарифмированием с оставлением целой части логарифма (log5123=2,99, т.е. m–1=2).
Далее:
b2 = 123 div 52 = 4; 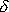 1 = 123 mod 52 = 23;
1 = 123 mod 52 = 23;
(i = 2 - 1 = 1);
b1 = 23 div 51 = 4; 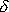 0 = 23 mod 51 = 3;
0 = 23 mod 51 = 3;
i = 0.
8.5. Алгоритмы перевода Zp 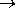 Z10
Z10
Необходимо Zp представить в форме многочлена и выполнить все операции по правилам десятичной арифметики.
Пример 3. Выполнить преобразование 4435 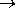 Z10
Z10
4435 = 4·52+4·51+3·50 = 4·25+4·5+3·1 = 12310.
Ситуация, однако, значительно упрощается, если основания исходной и конечной систем счисления оказываются связанными соотношением p = qr, где r – целое число (естественно, большее 1) или r = 1/n ( n>1, целое) – эти случаи будут рассмотрены ниже.
8.6. Перевод чисел между системами счисления 2 – 8 – 16
Двоичная система счисления используется для представления чисел в компьютере.
Однако двоичная запись оказывается громоздкой, поскольку содержит много цифр, и, кроме того, она плохо воспринимается и запоминается человеком из-за зрительной однородности (все число состоит из нулей и единиц).
Поэтому в нумерации ячеек памяти компьютера, записи кодов команд, нумерации регистров и устройств и пр. используются системы счисления с основаниями 8 и 16;
Выбор именно этих систем счисления обусловлен тем, что переход от них к двоичной системе и обратно осуществляется простым образом.
Двоичная система счисления имеет основанием 2 и, соответственно, 2 цифры: 0 и 1.
Восьмеричная система счисления имеет основание 8 и цифры 0, 1, ..., 7.
Шестнадцатеричная система счисления имеет основание 16 и цифры
0, 1, ..., 9, A, B, C, D, E, F.
При этом знак A является 16-ричной цифрой, соответствующей числу 10 в десятичной системе; B16 = 1110; C16 = 1210; D16 = 1310; E16 = 1410; F16 = 1510.
В данном случае A ... F - это не буквы латинского алфавита, а цифры 16-ричной системы счисления и поэтому они имеют только такое начертание (не могут быть представлены в виде, например, соответствующих строчных букв, как в текстах).
Пользуясь алгоритмами, сформулированными в предыдущих разделах, можно заполнить таблицу:
| Таблица 1. Представление чисел в системах счисления 2 – 8 – 16 |
| Основание системы счисления | |||
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Докааны две теоремы.
Теорема 1.
Для преобразования целого числа Zp 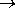 Zq в том случае, если системы счисления связаны соотношением q = pr, где r - целое число большее 1, достаточно Zp разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q.
Zq в том случае, если системы счисления связаны соотношением q = pr, где r - целое число большее 1, достаточно Zp разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q.
Пример 6. Выполнить преобразование Z2 = 1100012 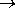 Z8.
Z8.
Исходное число разбивается на группы по три разряда справа налево (8 = 23, следовательно, r = 3) и каждая тройка в соответствии с таблицей 1 переводится в 8-ричную систему счисления независимо от остальных троек:
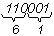
Следовательно, 1100012 = 618 .
Аналогично, разбивая Z2 на группы по 4 двоичные цифры и дополняя старшую группу незначащими нулями слева, получим 1100012= 3116.
Теорема 2.
Для преобразования целого числа Zp 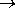 Zq в том случае, если системы счисления связаны соотношением p = qr, где r - целое число большее 1, достаточно каждую цифру Zp заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при необходимости незначащими нулями слева до группы в r цифр.
Zq в том случае, если системы счисления связаны соотношением p = qr, где r - целое число большее 1, достаточно каждую цифру Zp заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при необходимости незначащими нулями слева до группы в r цифр.
Пример 7. Выполнить преобразование D316 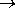 Z2.
Z2.
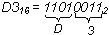
Переходы Z8 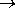 Z16 и Z16
Z16 и Z16 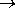 Z8, очевидно, удобнее осуществлять через промежуточный переход к двоичной системе. Например, 1238 = 0010100112 = 5316.
Z8, очевидно, удобнее осуществлять через промежуточный переход к двоичной системе. Например, 1238 = 0010100112 = 5316.
Дата добавления: 2015-07-22; просмотров: 1955;
