Кодирование и обработка в компьютере целых чисел без знака

Для записи числа в устройствах компьютера выделяется фиксированное количество двоичных разрядов.

Память компьютера имеет байтовую структуру, однако, размер одной адресуемой ячейки обычно составляет несколько байт.

Например, ячейка памяти объединяет 2 байта (16 двоичных разрядов) - такая комбинация связанных соседних ячеек, обрабатываемая совместно, называется машинным словом.

Для представления числа в регистре арифметико-логического устройства процессора, где формируется результат операции, имеется еще один дополнительный одноразрядный регистр, который называется регистром переноса и который можно рассматривать в качестве продолжения (т.е. 17-го бита) регистра результата.

Назначение этого бита выяснится чуть позже.

Конечный размер разрядной сетки порождает понятие "наибольшее целое число", которого в обычном (немашинном) представлении чисел просто не существует.

Если количество разрядов k и основание системы счисления p=2, то (Z₂)_max = 2^{k - 1}.

В частности, при k=16 (Z₂)_max = 2^{16 - 1} = 111 1111 1111 1111₂ =65535₁₀.

Таким образом, целого числа, например 65636 и более в компьютере просто не может существовать и, следовательно, появление в ходе вычислений чисел, превышающих (Z₂)_max, должно интерпретироваться как ошибка.

Минимальным целым числом в беззнаковом представлении является (Z₂)_min = 000 0000 0000 0000₂ = 0₁₀.

В языке программирования PASCAL целые числа без знака, для записи которых отводится 2 байта, определены как тип Word.

Тип числа устанавливает способ кодирования этого числа, то есть количество отводимых для записи ячеек памяти (т.е. разрядность числа), а также перечень допустимых операций при обработке.

Выход за границу 65535 возможен только путем увеличения количества разрядов для записи числа, но это порождает новый тип со своим Z_max; например, тип Longint ("целое число со знаком") с максимальным значением 2147483647₁₀, числа которого занимают 4 байта.

С беззнаковыми числами выполняются арифметические операции, не меняющие типа числа; к которым относятся сложение и умножение.

Сложение

Сложение производится согласно таблице сложения, которая для двоичных чисел имеет вид:

В последнем случае в том разряде, где находились слагаемые, оказывается 0, а 1 переносится в старший разряд и называется битом переноса..

Пример 1. Найти сумму 1594₁₀ + 17563₁₀ при беззнаковой двоичной кодировке и 16-битном машинном слове.

После перевода слагаемых в двоичную систему счисления и выполнения сложения получим (для удобства восприятия 16-ти разрядное число разобьем на группы по четыре разряда):

1 11 --Переносы

0010 0110 1001 0100

0011 0000 0011 1001

0 0101 0110 1100 1101

Рег. переполнения

Пример 2. Найти сумму 65534₁₀ + 3₁₀

1111 1111 1111 11 ---Переносы

1111 1111 1111 1110

0000 0000 0000 0011

1 0000 0000 0000 0001

Рег. переполнения

В последнем примере в результате сложения получилось число, превышающее максимально возможное, то есть результат ошибочен, о чем свидетельствует появление 1 в регистре переполнения.

Возникновение такой ситуации в ходе выполнения программы, написанной на языке, где предусмотрено строгое описание типа переменных, приводит к прекращению работы и выводу сообщения об ошибке.

В программах, предназначенных для обработки числовой информации (например, Excel, MathCAD или Calc), при переполнении разрядной сетки производится автоматическое преобразование целого числа в вещественный тип.

Таким образом, регистр переполнения в данном случае служит индикатором корректности процесса вычислений.

Умножение

Умножение производится согласно таблице умножения, которая для двоичных чисел имеет следующий вид:

0 · 0 = 0
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1

Пример 1. Найти произведение 13₁₀ × 5₁₀ . После перевода сомножителей в двоичную систему счисления получим

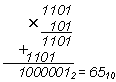
Таким образом, умножение двоичных чисел сводится к операциям сдвига на один двоичный разряд влево и повторения первого сомножителя в тех разрядах, где второй сомножитель содержит 1, и сдвига без повторения в разрядах с 0.

Сдвиг всегда чередуется со сложением из-за ограниченности числа регистров, которые имеются в процессоре для размещения операндов. Другими словами, реализации отдельной операции умножения в процессоре не требуется.

Как и в операции сложения, при умножении чисел с ограниченной разрядной сеткой может возникнуть переполнение. Решается проблема рассмотренными выше способами.