Профильные потери.

а) потери на трение.

При течении через решетку профилей вязкой жидкости вокруг стенок сопла или лопаток образуется пограничный слой, в котором и происходят потери. Типичная картина распределения скоростей по поперечному сечению соплового канала показано на рисунке, где нанесены линии равных коэффициентов .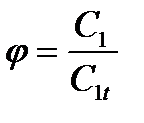

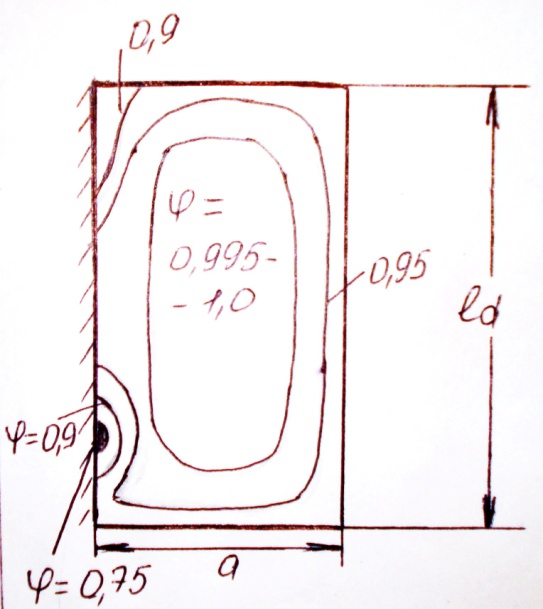
Из рисунка следует, что в ядре потока потери почти отсутствуют и трение имеет место лишь в пограничном слое. В углах соплового канала на спинке профиля значения коэффициентов φ минимальны. Это объясняется наличием в этих местах вихрей.

Потери трения в пограничном слое зависят от того, является ли пограничный слой ламинарным или турбулентным. Сопла и лопаточные профили должны проектироваться таким образом, чтобы точка перехода ламинарного пограничного слоя в турбулентный находилась как можно дальше от передней кромки профиля, т.е. необходимо стремиться к образованию ламинарного пограничного слоя на большем участке профиля.

Структура пограничного слоя при обтекании лопатки вязкой жидкостью показана на следующем рисунке.

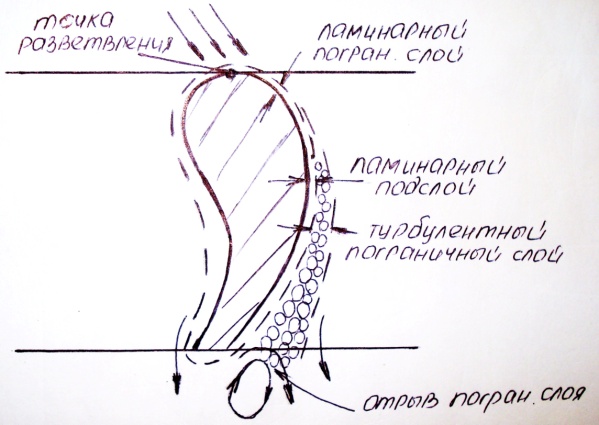
Сопротивление трения в значительной мере зависят так же от состояния поверхности стенок профиля и числа Рейнольдса – Rе. Особенно значительные потери вызываются отрывом пограничного слоя от профиля.

б) Потери, связанные с отрывом пограничного слоя.

Потери, связанные с отрывом пограничного слоя от профиля решетки в значительной мере зависят: от угла атаки i, с которым поток набегает на входную кромку профиля; от формы профиля и от шага решетки, формирующих форму рабочего канала.

1) Влияние угла атаки i

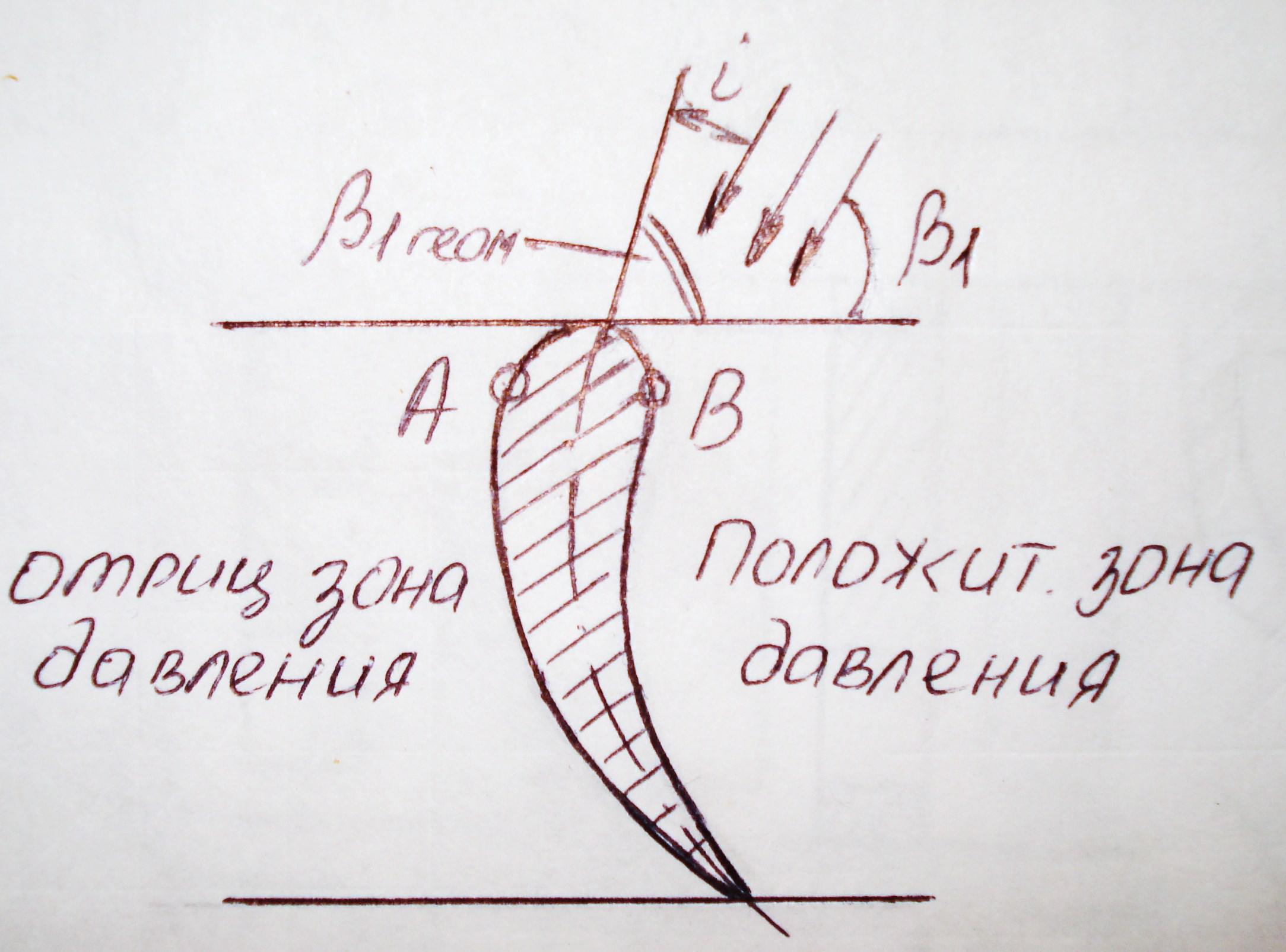
При положительных углах атаки 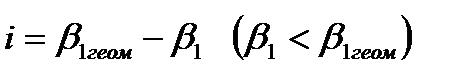минимум давления на выпуклой поверхности профиля перемещается к передней кромке в точку А и возрастает по абсолютной величине.

В соответствии с законом Бернулли на этом участке профиля возникают большие скорости потока. Это явление усиливается при малом радиусе кривизны кромки профиля. Резкое понижение давления вызывает местный срыв потока. При сравнительно небольших углах атаки этот местный срыв может не повлечь общего срева потока, но лобовое сопротивление профиля возрастает. При некотором угле атаки , называемом критическим, происходит общий срыв потока и дальнейшее увеличение угла атаки вызывает падение подъемной силы профиля.

Опыт показывает, что при 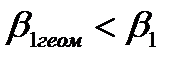уменьшается степень реактивности решетки, увеличивается неравномерность поля скоростей и давлений в канале, что приводит к увеличению толщины пограничного слоя и изменению его структуры, а часто к отрыву потока и возникновению вихревой зоны на спинке профиля.

В активных лопатках с некоторой степенью реактивности потери при уменьшении β будут тем выше, чем меньше начальная степень реактивности на расчетном режиме.

При отрицательных углах атаки ( 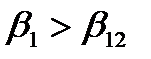) происходит понижение давления на вогнутой стороне профиля вблизи входной кромки (точка В), что может вызвать местный срыв потока и послужит причиной повышения лобового сопротивления.

На выпуклой же стороне профиля при отрицательных углах атаки неравномерность поля скоростей и довлений уменьшается, что улучшает условия обтекания профиля вдоль этой поверхности и уменьшает опасность отрыва струи у входной кромки. Отрыв обычно имеет место на вогнутой стороне профиля, но в зоне небольших скоростей. Поэтому потери в этом случае будут меньше. Т.о. обтекание профиля при отрицательных углах атаки может дать лучшие результаты.

Надежной оценкой потерь энергии в лопаточном аппарате при обтекании профилей под различными углами атаки является эксперимент в условиях, близких к действительной работе ступени.

Ниже на рисунке дан характер изменения коэффициента ψ от угла β₁ , натекания струи на профиль при постоянном значении выходных углов .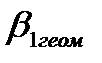

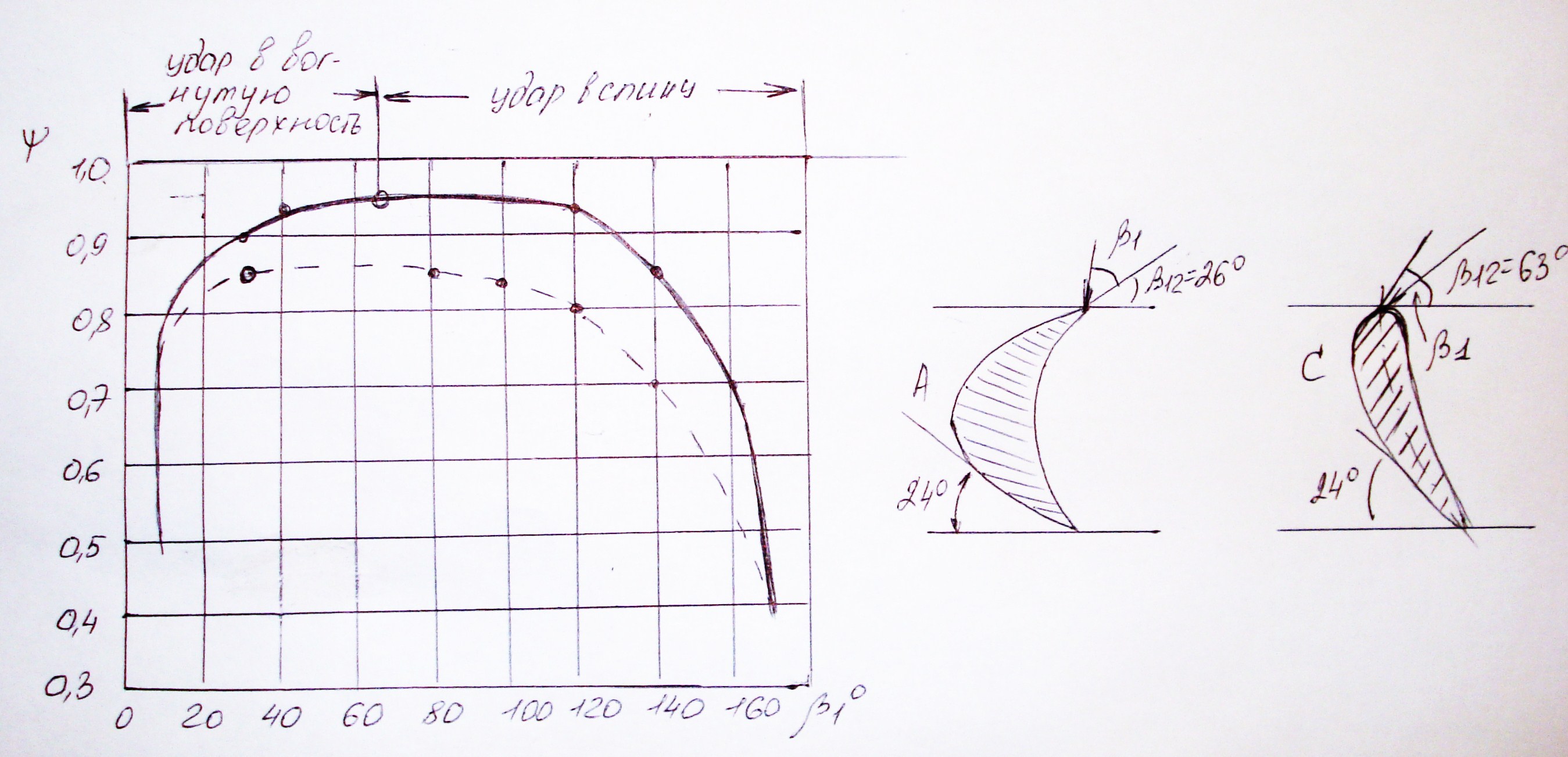
На кривых отмечена точка, соответствующая «безударному» входу, т.е.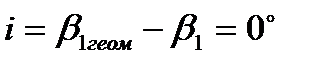

В обоих случаях в этих точках мы имеем максимальные значения ψ.

Из рисунка следует, что при «ударе» в вогнутую поверхность коэффициент ---- падает более резко, чем при «ударе» в спинку.

2) Влияние формы профиля

Потери трения на профиле, как указывалось выше , зависят от того, является ли пограничный слой ламинарным или турбулентным. Характер пограничного слоя на профиле в первую очередь зависит от аэродинамических качеств профиля. Раньше к форме профиля не предъявляли особых условий и выполняли их таким образом, чтобы они удовлетворяли только выбранным углам входа и выхода. При этом спинка и вогнутая поверхность профиля обычно описывались самыми элементарными методами: двумя прямыми и частью окружности.

Два профиля, нарисованные на рисунке, считались равноценными для обтекания их потоком. Однако, развитие аэродинамики показало, что характер обтекания профиля при больших углах атаки в значительной мере зависит от формы выпуклой поверхности и конструкции передней кромки профиля. Опыт показывает, что при обтекании профилей с толстой входной кромкой к.п.д. профиля остается неизменным при широком диапазоне изменения угла атаки. С другой стороны такие профили дают большее сопротивление, чем тонкие при нулевом значении угла атаки. Кроме того выяснилось,что выпуклая сторона контура профиля должна очерчиваться плавной кривой и не иметь прямолинейных участков.

Новые профили, созданные в период с 1950 – 53г. ЦКТИ, Кировским заводом, ЛМЗ, НЗЛ позволяют получить более совершенную проточную часть турбины и увеличить к.п.д. турбины на 2 – 3% и более.

Преимущества новых типов профилей хорошо иллюстрируются рисунком

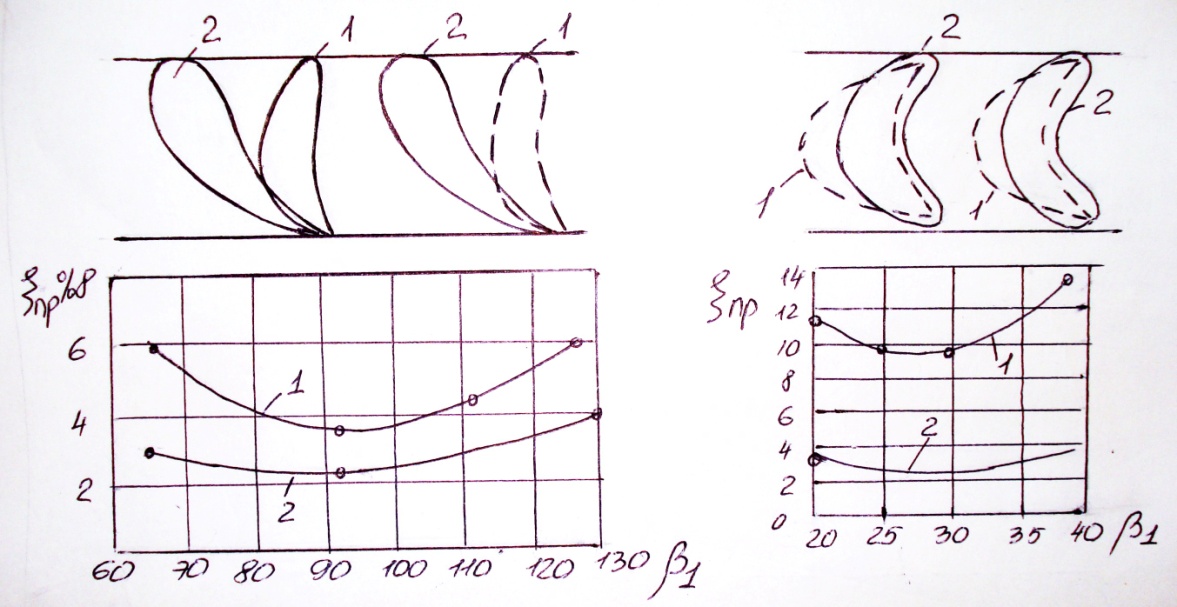
Изменение профильных потерь ξ_пр в зависимости от угла натекания потока β₁:

а) направляющие лопатки; б) рабочие лопатки

1 – старые профили; 2 – новые профили.

3) Влияние относительного шага на условия обтекания.

С изменением шага лопаток существенно изменяются и условия обтекания потоком профиля. Поэтому для каждой формы профиля существует вполне определенная оптимальная величина относительного шага, которую называют оптимальным шагом.

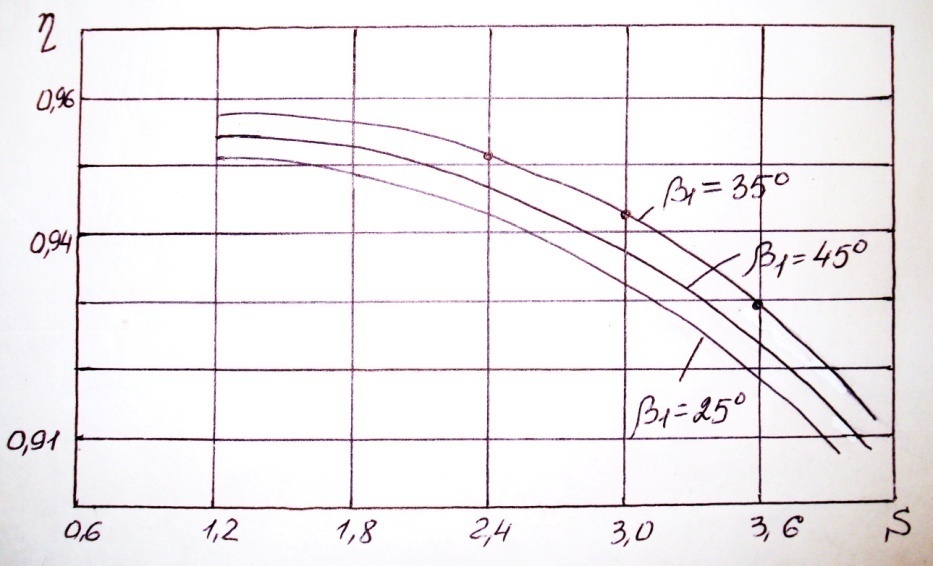
Ниже на рисунке даны кривые изменения коэффициента ψ² для решетки активных лопаток в зависимости от величины относительного шага и угла атаки.

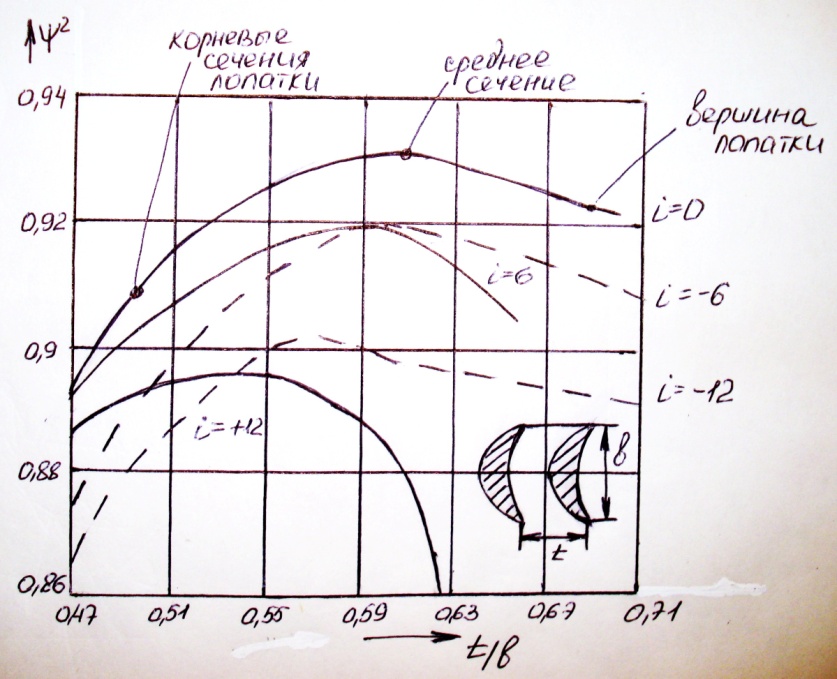
Оптимальное значение относительного шага получается тем меньше, чем больше по абсолютной величине угол атаки. Чем болше угол атаки, тем резче выражен минимум потерь (т.е. тем меньше выбор величины относительного шага). При отрицательных углах атаки в области больших значений относительного шага потери энергии меньше.

При сильном отклонении от оптимального шага потери резко растут, что объясняется возникновением диффузарных участков на профиле. При изменении шага лопаток будет меняться форма канала. Это приводит в активных каналах к появлению диффузорных и конфузорных участков (конфузорный эффект – увеличение скорости, диффузорный эффект – уменьшение скорости), которые могут служить причиной возникновения значительных потерь энергии.

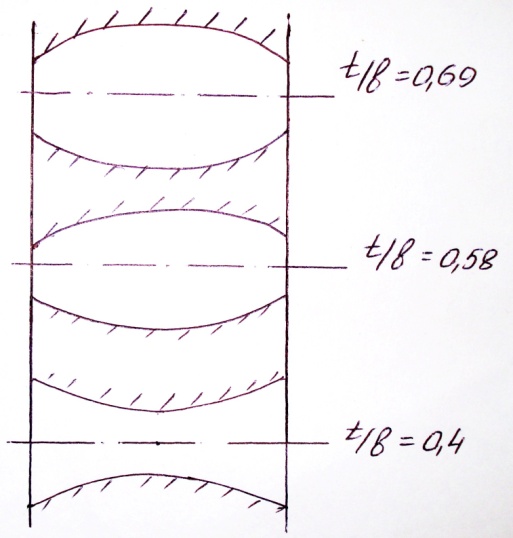
Так как диффузорный эффект возникает как при увеличении так и при уменьшении шага активных лопаток, то для этого типа лопаток получается довольно резко выраженный минимум потерь энергии при определенном относительном шаге.

При изменении шага реактивных лопаток межлопаточный канал остается суживающимся при значительных изменениях шага. В связи с этим кривая изменения потерь энергии в зависимости от шага плоучается вблизи минимума потерь энергии очень полной, что является преимуществом реактивных лопаток.

Обычно для реактивных лопаток 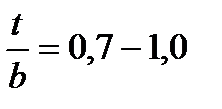, а для активных .

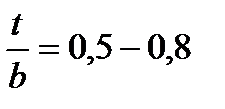При статической продувке профилей очень часто определяют к.п.д. профиля в зависимости от величины относительного шага .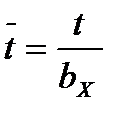

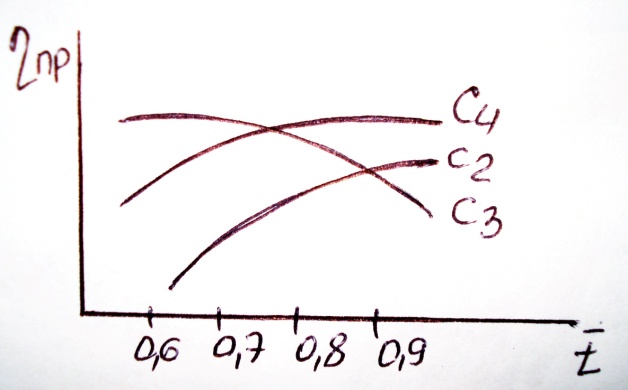
Для современных профилей зависимость потерь от шага имеет несколько другой характер.

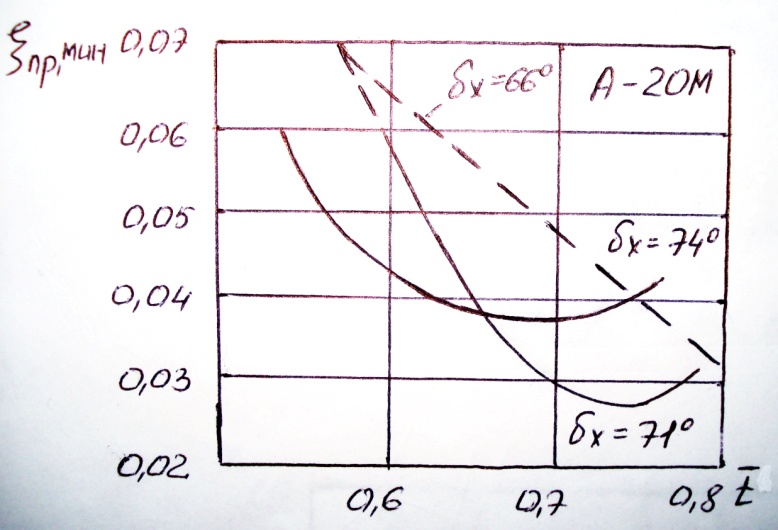
Минимум потерь смещается в сторону больших величин , что хорошо видно на рисунке, где дана зависимость ξ_{кр мин} при безударном обтекании профиля А – 20М.

в) Кромочные потери

Третью часть профильных потерь составляют вихревые потери за выходной кромкой или так называемые кромочные потери.

За выходной кромкой решетки в результате отрыва потока возникают вихри, образующие кромочный след. По опытным данным выравнивание потока за решеткой происходит достаточно интенсивно и практически заканчивается на расстоянии y = (1,3÷1,9)t от выходных кромок. На выравнивание потока затрачивается определенная энергия. На малых расстояниях за выходными кромками поток имеет неравномерные поля скоростей, давлений и углов.

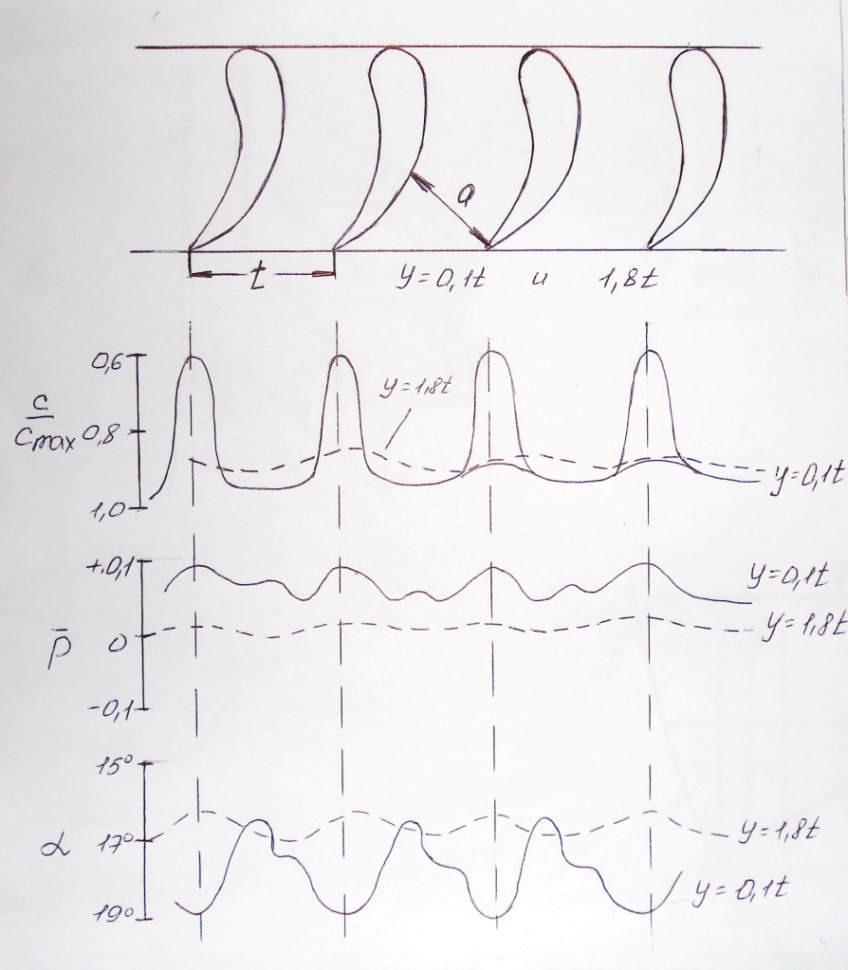
Углы выхода потока из решетки относятся к важнейшим характеристикам потока, так как от них зависит величина вращающего момента в уравнении Эйлера.

Конечная толщина кромки лопаток вызывает уменьшение угла выхода по сравнению с геометрическим – струя несколько отклоняется от направления, диктуемого очертанием выходных кромок. Обычно средний угол выравнившегося потока за решеткой обозначают или α_1эф и β_2эф или просто α₁ и β₂. Углы α₁ и β₂ часто не совпадают с геометрическими углами профиля лопатки.

Средние углы выравнившегося потока за решеткой определяют обычно экспериментально. Иногда пользуются эмпирической формулой

;

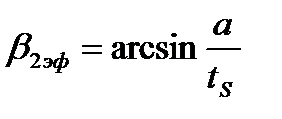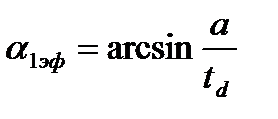
В формулах 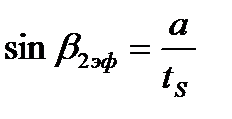и 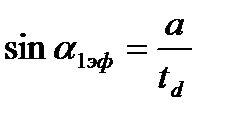очень часто при малых докритических скоростях истечения принимается поправочный коэффициент 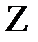и они записываются так

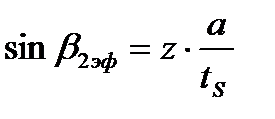и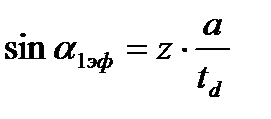

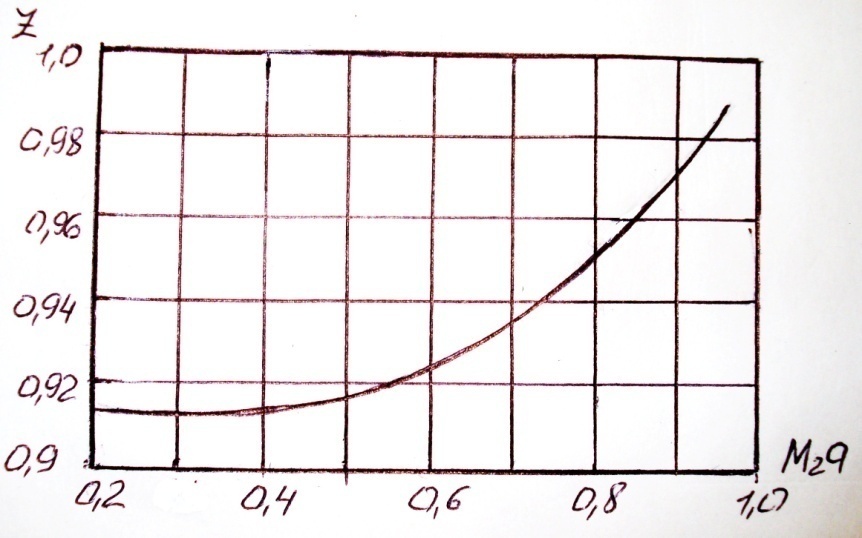
Значение Z можно брать по графику Эйнли (И.В.Котляр «Переменные режимы работы газотурбинных установок»).

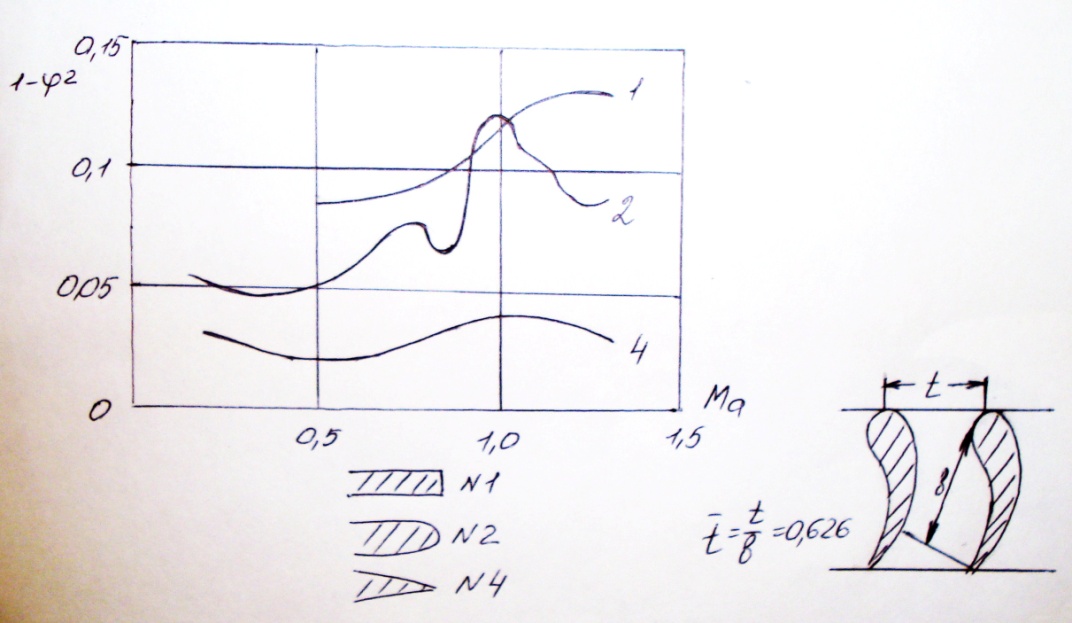
Потери от срыва потока с выходной кромки зависят от формы и толщины выходной кромки профиля и от скорости.

На рисунке даны зависимости потерь от скорости потока и от формы кромки.

Изменение потерь энергии в зависимости от толщины выходной кромки турбинных активных лопаток показано на рисунке.

Коэффициент кромочных потерь до последнего времени определяется по уравнению

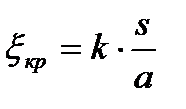
где s – толщина кромки

а – ширина канала

k = 0,1÷0,4 – коэффициент, определяемый экспериментальным путем

Г.Ю. Степанов рекомендует определять кромочные потери по формуле Флигеля

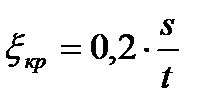
Углы выхода потока α₁ и β₂ зависят от эффективных (геометрических) углов, конфигураций решетки и режима обтекания.

Для дозвуковых скоростей

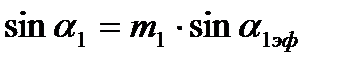
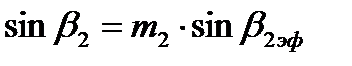
где

Здесь μ₁ и μ₂ - коэффициент расхода (отношение действительного расхода через решетку к теоретическому, подсчитанному по изоэнтропийным параметрам 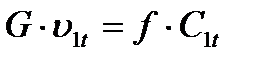). Значения μ, φ и ψ для предварительных расчетов можно брать в книге Б.М.Трояновского «Турбины для АЭС».

Величины эффективных углов α_1эф и β_2эф определяются обычно при продувке профиля в зависимости от относительного шага 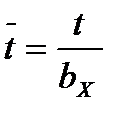и угла установки профиля δ_х.