Расширение пара в косом срезе

Выходная часть турбинного сопла наклонена к плоскости движения лопаток под углом

α₁. Вследствие этого за выходной частью сопла получается косой срез. Оказывается, что в этом случае в суживающихся соплах можно получить сверхкритические скорости за счет дополнительного расширения в косом срезе. В суженно-расширенных соплах с косым срезом можно получить скорости выше тех, на которые было рассчитано сопло. При расширении пара в косом срезе происходит отклонение струи в сторону, обратную косой стенке.

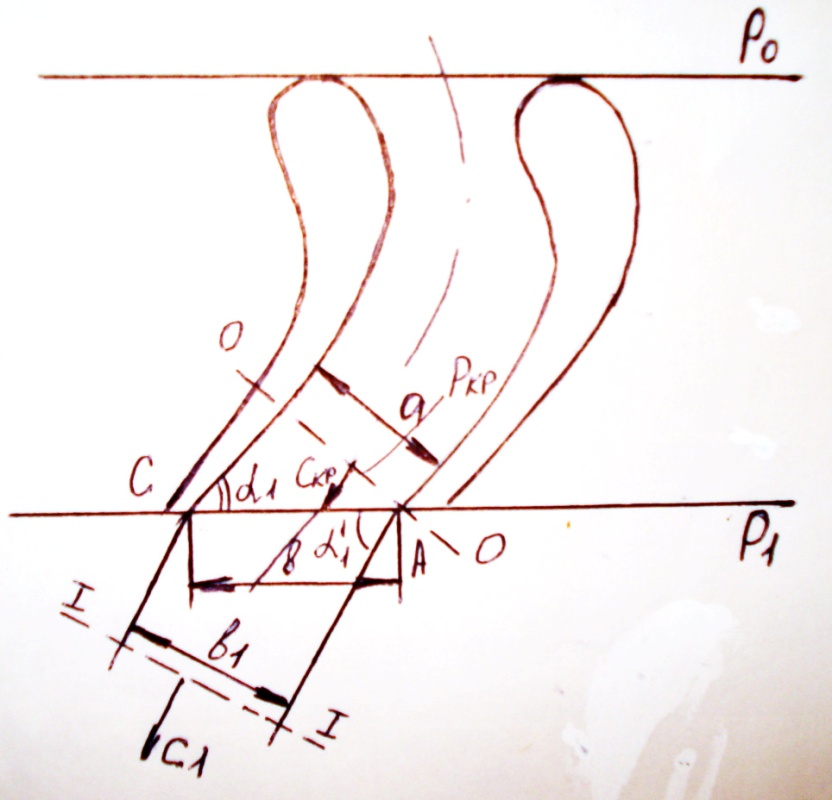
Физическая сущность явления заключается в следующем: в докритических сечениях сопла скорость нарастает быстрее, чем удельный объем. После критического сечения наоборот, т.е. струя должна расширяться, но этому расширению частично препятствует стенка ВС. В точке А давление скачком падает от Р_кр до Р₁, а по стенке ВС давление падает постепенно, что вызывает силу, которая отклоняет струю.

При определении параметров потока за косым срезом и угла наклонения струи пользуются методами газодинамики и уравнением сплошности.

Поскольку расход в сечениях О-О и I-I одинаков, на основании уравнения сплошности можно написать

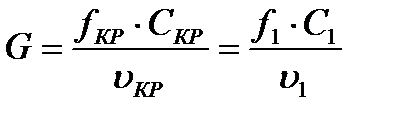(1)

Здесь:

площадь струи в критическом сечении при высоте сопла l_d

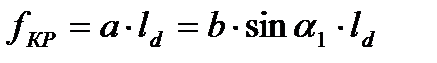
(2)

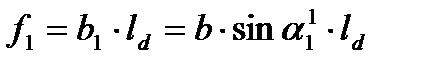
Тогда

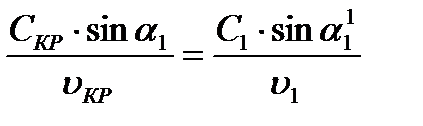, откуда

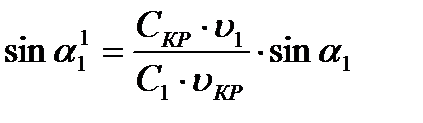(3)

Угол отклонения струи

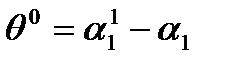(4)

Формулу (3) можно представить, выразив ее через давление и степень расширения пара в сопле.

Подставим

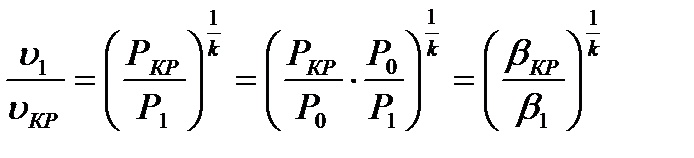
т.к.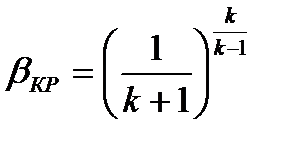

получим

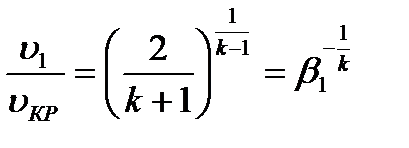
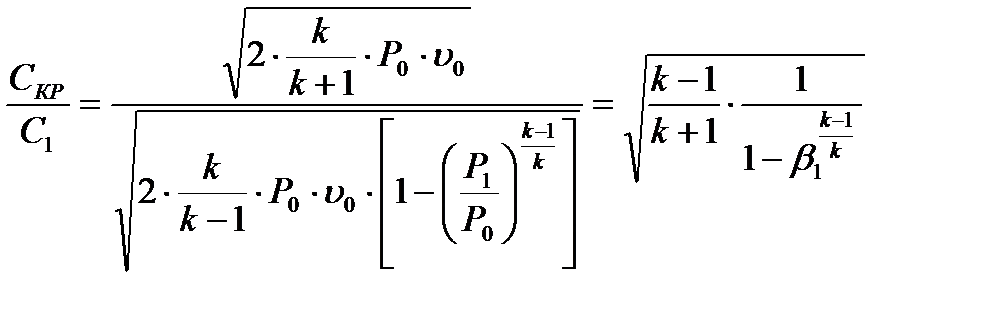
Тогда

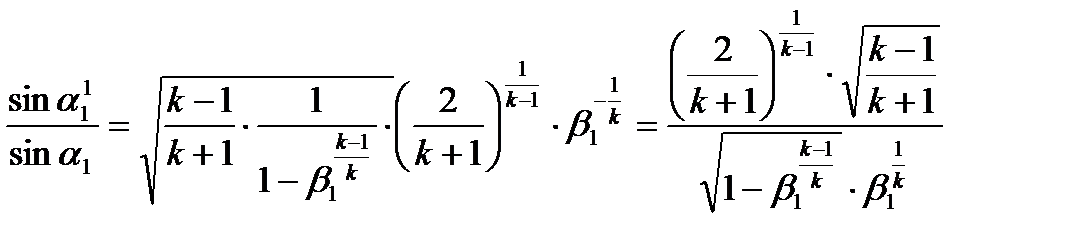(5)

Таким образом, на основании уравнения неразрывности можно приблизительно установить зависимость между отклонением струи в косом срезе и степенью расширения.

См. Дейг «Технологическая газодинамика»

Дейг, Самойлович «Основы аэродинамики осевых турбомашин».

Следует подчеркнуть, что пар в косом срезе может расширяться лишь до известного предела и найденные зависимости можно применить лишь для определенных значений 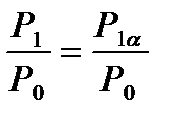(если скорость не превосходит критическую больше, чем на 70%).

Предельное понижение давления в косом срезе 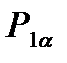можно определить из уравнения (3) используя основные положения курса газодинамики.

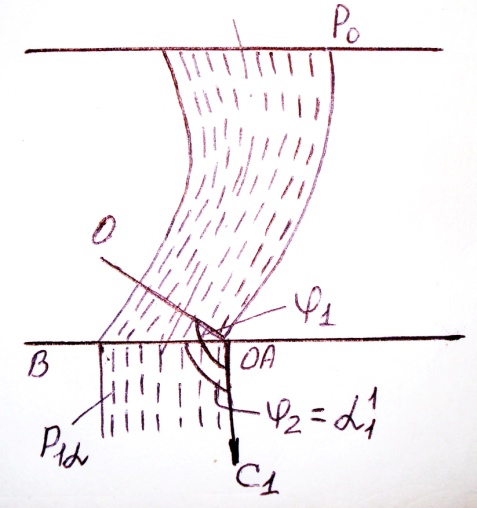
При предельном расширении давлении на линии АВ косого среза будет точно равно противодавлению 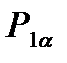(т.е. за косым срезом расширение отсутствует). В этом случае волна Маха, на которой заканчивается преобразование потока, должна совпадать с линией АВ и угол Маха φ₂ равен углу α¹₁ = α₁ + θ (другая волна должна совпадать с направлением О-О ).

Тогда

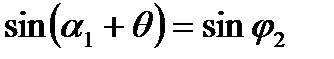
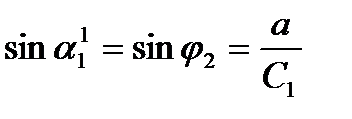, где 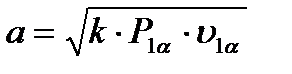- скорость звука

Отсюда

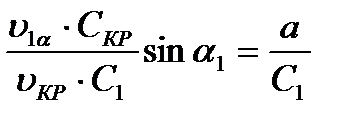
Заменяя 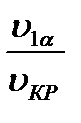и сокращая на С₁ получим

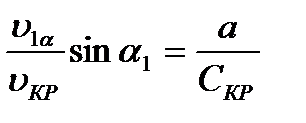или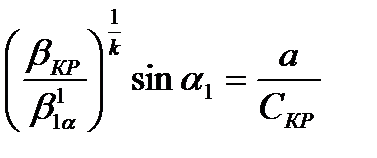

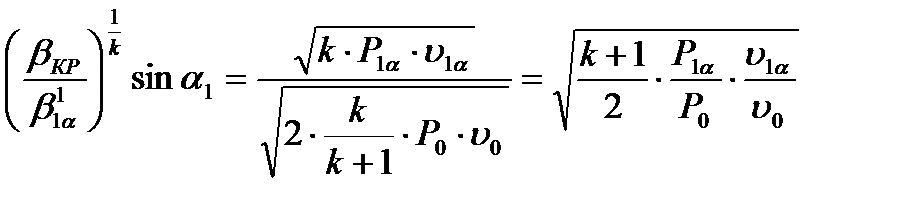
Здесь

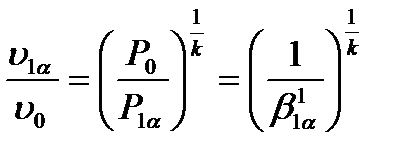и 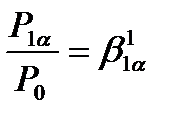, тогда

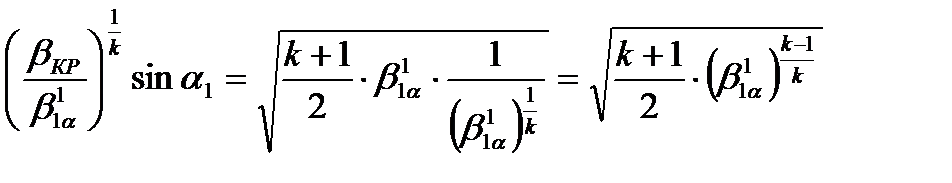
Решая относительно 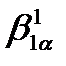найдем предельное отношение давлений, срабатываемое в косом срезе.

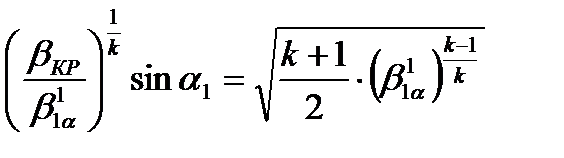
Возводим в квадрат

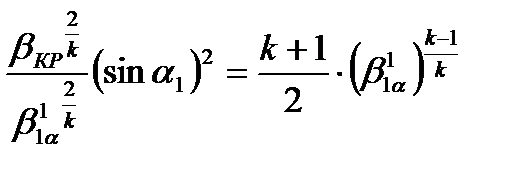
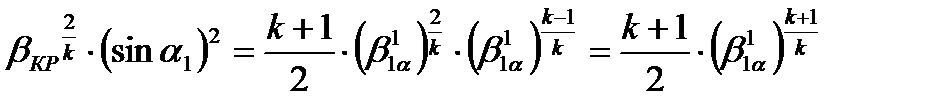
Отсюда

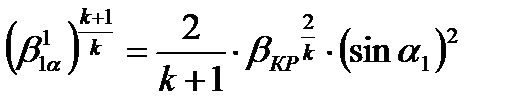
или

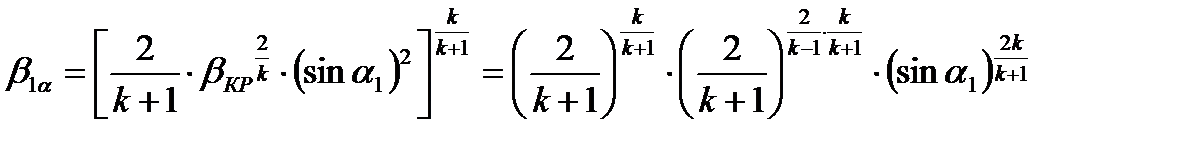
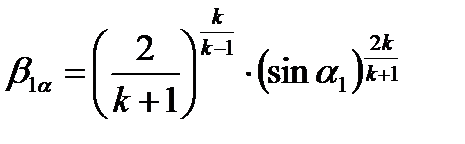
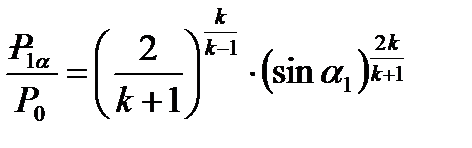(6)

При расширении газа до противодавления меньшего Р_1α, происходящем уже за пределами сопла, скорость газа и угол отклонения струи, как показал флюгель, продолжает увеличиваться. Однако окружная скорость составляющая С_1u при этом не возрастает, а следовательно не увеличивается и работа турбины.

Диаграмма изменения вектора скорости С₁ при изменении противодавления Р₁ показана на рисунке.

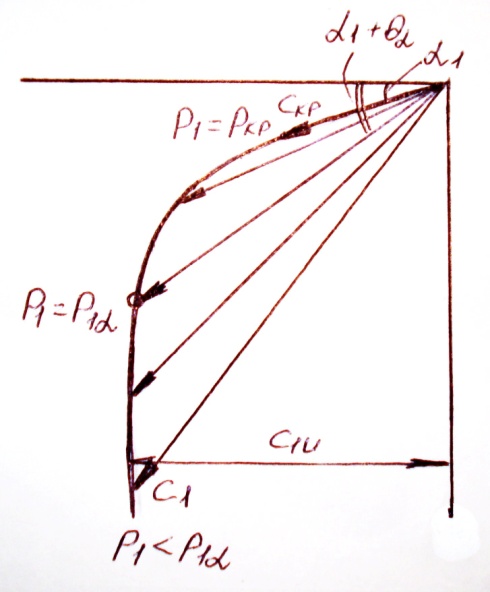
Если Р₁ = Р_кр, то газ выходит из сопла под углом α₁ со скоростью С_кр. При уменьшении Р₁ скорость возрастает, но появляется угол отклонения струи, достигающий значения θ₁ при

Р₁ = Р_1α.

При дальнейшем снижении противодавления вплоть до нуля скорость С₁ и угол θ возрастают, но окружная скорость С_1u остается постоянной, и окружная мощность не возрастает.

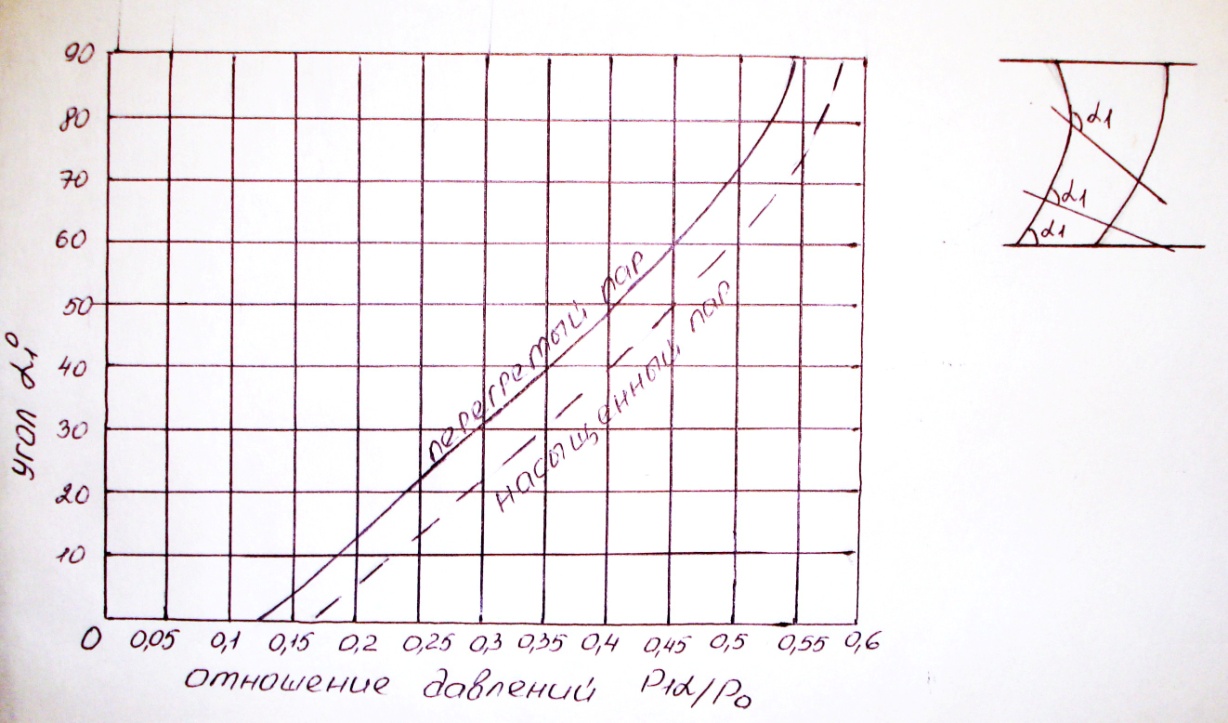
Величину наибольшего расширения можно определять пользуясь графиком.