Понятие об электронной теории дисперсии
Явление дисперсии может быть объяснено на основе электромагнитной теории и электронной теории вещества. Из электромагнитной теории Максвелла следует, что абсолютный показатель преломления прозрачной среды (m»1) определяется формулой
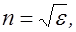 (2.19.4)
(2.19.4)
где e - диэлектрическая проницаемость среды.
На первый взгляд может показаться, что формула (2.19.4) противоречит данным опыта. Так, например, для воды e = 81 и, следовательно, показатель преломления должен быть равен девяти.
Из опыта следует, что для видимого света абсолютный показатель преломления воды равен 1,33.
Отмеченное "противоречие" не связано с недостатками теории Максвелла, а является следствием того, что не учитывается зависимость диэлектрической проницаемости e от частоты. В стационарном электрическом поле преобладает ориентационная поляризация. В переменном поле молекулы воды не могут мгновенно изменить свою ориентацию, поэтому при низких частотах величина e будет близка к 81. В переменных полях достаточно большой частоты (n»1015Гц) ориентационная поляризация воды или любого упругого диэлектрика с полярными молекулами будет практически отсутствовать. Для видимого света величина относительной диэлектрической проницаемости среды обуславливается только электронной поляризацией, то есть колебаниями электронов в атомах или молекулах под действием электромагнитной волны. Движение электронов в атомах подчиняются законам квантовой механики, однако, как показал Лоренц, для качественного понимания многих оптических явлений достаточно ограничиться гипотезой о существовании внутри атомов и молекул электронов, связанных квазиупруго.Будучи выведены из положения равновесия, электроны начнут колебаться, постепенно теряя энергию колебаний на излучение электромагнитных волн. Затухание колебаний можно учесть, введя "силу трения", пропорциональную скорости. При прохождении через вещество электромагнитной волны каждый электрон оказывается под действием электрической силы, изменяющейся по закону:
f=eEmcos(wt+j),(2.19.5)
где Em - амплитуда напряженности электрического поля волны; j - величина, определяемая координатами данного электрона.
Под воздействием этой силы электрон начинает совершать вынужденные колебания, амплитуда (rm) и фаза (a) которых определяются формулами:
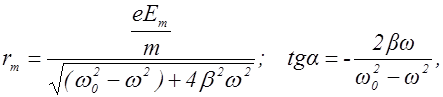 (2.19.6)
(2.19.6)
где wo - собственная частота колебаний электрона;
b - коэффициент затухания.
Колеблющийся электрон возбуждает вторичную волну, распространяющуюся с фазовой скоростью С. Вторичные волны, складываясь с первичной, образуют результирующую волну. Фазы вторичных волн отличаются от фазы первичной волны (формула 2.19.6), поэтому результирующая волна распространяется в веществе с фазовой скоростью V, отличной от скорости волн в пустоте. Различие между V и С будет тем больше, чем ближе частота волны к резонансной частоте электронов. Отсюда вытекает существование зависимости V от w, то есть дисперсия.
Для упрощения расчетов, затуханием колебаний за счет излучения вначале пренебрежем. Положив в формулах (2.19.6) b = 0, получим:

Таким образом, при отсутствии затухания колебания электрона описывается уравнением

Учитывая, что мгновенное значение напряженности электрического поля в данной точке вещества равно E(t)=Emcos(wt+j),мгновенное значение смещения электрона из положения равновесия можно представить в виде
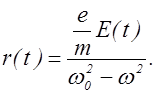
В результате смещения электронов (смещение ядер пренебрежимо мало) из положений равновесия молекула приобретает электрический дипольный момент:
 (2.19.7)
(2.19.7)
В этом выражении суммирование производится по всем электронам, входящим в состав молекулы. Направление смещений 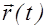 совпадает с направлением поля
совпадает с направлением поля 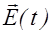 , поэтому векторное сложение заменено алгебраическим.
, поэтому векторное сложение заменено алгебраическим.
Мгновенное значение модуля вектора поляризации вещества найдем, умножив Р(t) на число молекул в единице объема N:
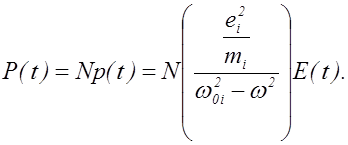 (2.19.8)
(2.19.8)
Диэлектрическая проницаемость вещества может быть представлена выражением
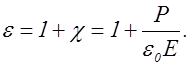
Подставив в это выражение отношение 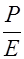 из (2.19.7) и заменяя согласно (2.19.4) e на n2, получим формулу
из (2.19.7) и заменяя согласно (2.19.4) e на n2, получим формулу
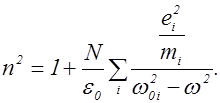 (2.19.8)
(2.19.8)

|
При значениях частоты волны w, заметно отличающихся от всех собственных частот w0i, сумма в (2.19.8) будет мала по сравнению с единицей, так что n2»1. Вблизи каждой из собственных частот функция (2.19.8) терпит разрыв: при w®w0i она обращается в +¥, если w<w0i, и в -¥ если w>w0i.
Такое поведение функции обусловлено тем, что мы пренебрегли затуханием (полагали b=0). Когда b¹0, амплитуда при всех значениях w остается конечной. Учет затухания приводит к зависимости n2 от w, представленной на рис. 2.19.3.
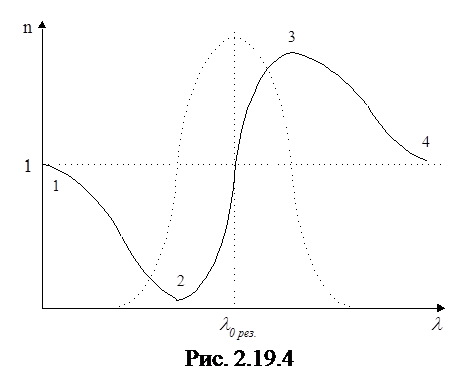 |
На рис.2.19.3 пунктиром показан ход функции (2.19.8). Если перейти от n2 к n и от w к l, то получим кривую, представленную на рис. 2.19.4 (показан участок кривой в области одной из резонансных длин волн).
Пунктирная кривая изображает ход коэффициента поглощения света веществом (§ 2.19.3). Участок 3-4 аналогичен кривой, приведенной на рис.2.19.1. Участки 1-2 и 3-4 соответствуют нормальной дисперсии 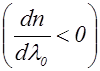 . На участке 2-3 дисперсия аномальна
. На участке 2-3 дисперсия аномальна 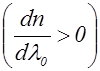 . В области 1-2 показатель преломления меньше единицы, следовательно, фазовая скорость волны превышает С. Это не противоречит теории относительности, основывавшейся на утверждении, что скорость передачи сигнала не может превысить С.Ранее (§ 2.5) отмечалось, что передать сигнал с помощью идеально монохроматической волны невозможно. Передача энергии (т.е. сигнала) с помощью не вполне монохроматической волны (группы волн) осуществляется с групповой скоростью, равной
. В области 1-2 показатель преломления меньше единицы, следовательно, фазовая скорость волны превышает С. Это не противоречит теории относительности, основывавшейся на утверждении, что скорость передачи сигнала не может превысить С.Ранее (§ 2.5) отмечалось, что передать сигнал с помощью идеально монохроматической волны невозможно. Передача энергии (т.е. сигнала) с помощью не вполне монохроматической волны (группы волн) осуществляется с групповой скоростью, равной
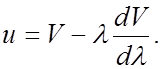
В области нормальной дисперсии 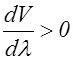 (dn и dV имеют разные знаки, а
(dn и dV имеют разные знаки, а 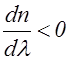 ), так что, хотя V>С, групповая скорость оказывается меньше С. В области аномальной дисперсии понятие групповой скорости теряет смысл (поглощение очень велико). Соответствующий расчет дает и в этой области для скорости передачи энергии значение, меньшее С.
), так что, хотя V>С, групповая скорость оказывается меньше С. В области аномальной дисперсии понятие групповой скорости теряет смысл (поглощение очень велико). Соответствующий расчет дает и в этой области для скорости передачи энергии значение, меньшее С.
Если электромагнитная волна распространяется не в диэлектрической среде, а в среде где в заметном количестве присутствуют свободные электроны (металлы, ионосфера), то в формуле (2.19.8) необходимо собственную частоту колебаний свободного заряда w0i положить равной нулю.
В этом случае формула (2.19.8) переходит в следующую:
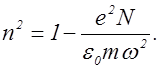 (2.19.9)
(2.19.9)
Концентрация электронов в ионосфере принимает случайные значения, поэтому и коэффициент преломления не имеет постоянного значения.
При больших частотах w показатель преломления стремится к единице и, следовательно, волны будут свободно проходить ионосферу, не преломляясь и не отражаясь на ее границах. Это ограничивает применение ЭМВ для радиосвязи, но открывает возможность для космической радиосвязи, радиолокации планет Солнечной системы и лежит в основе радиоастрономии, использующей волны УКВ диапазона.
При значениях 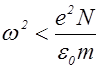 показатель преломления становится мнимым. Последнее означает, что длинные радиоволны не могут проникать в металл или ионосферу. Так как длинные радиоволны отражаются от ионосферы, то их используют для дальней связи за пределами прямой видимости.
показатель преломления становится мнимым. Последнее означает, что длинные радиоволны не могут проникать в металл или ионосферу. Так как длинные радиоволны отражаются от ионосферы, то их используют для дальней связи за пределами прямой видимости.
Дата добавления: 2015-07-22; просмотров: 1511;
