Закон Малюса

Естественный и поляризованный свет.

Реальная световая волна, как отмечалось ранее (§2.10) слагается из множества цугов волн, испускаемых отдельными атомами. Плоскость колебаний вектора 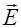для каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания вектора 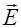различных направлений представлены с равной вероятностью
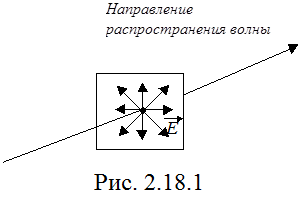
(рис. 2.18.1.)

Такая световая волна называется естественной. Световая волна, в которой направления колебаний вектора 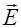каким-либо образом упорядочены, называется поляризованной.

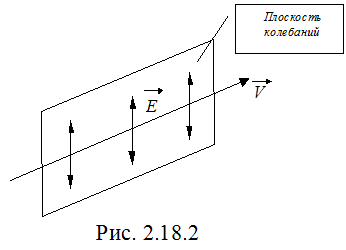
Если колебания вектора 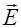происходят только в одной плоскости (рис. 2.18.2), световая волна называется плоско - (или прямолинейно) поляризованной.

Плоскополяризованную волну можно получить из естественной с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания, параллельные плоскости, которую называют плоскостью поляризатора и полностью задерживают колебания, перпендикулярные к этой плоскости. Колебание с амплитудой 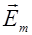, совершающееся в плоскости, образующей угол j с плоскостью поляризатора, можно разложить на два колебания с амплитудами
(рис. 2.18.3)

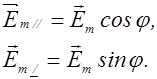
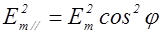Первое колебание пройдет через прибор, а второе будет задержано. Интенсивность прошедшей волны пропорциональна , то есть равна j_mcos²j, где j_m - интенсивность колебания с амплитудой 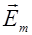. Таким образом, колебание, параллельное плоскости поляризатора, несет с собой долю интенсивности, равную 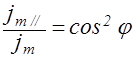. В естественном свете все значения j равновероятны. Поэтому доля света, прошедшего через поляризатор, будет равна среднему значению cos²j, то есть 1/2.

Если вращать поляризатор вокруг направления естественного луча, интенсивность прошедшего света не будет меняться, изменяется лишь ориентация плоскости колебаний вектора .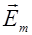

Пусть на поляризатор падает плоскополяризованный свет с амплитудой 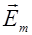и интенсивностью j_m (рис. 2.18.4).

Через поляризатор пройдет составляющая колебания с амплитудой E=E_mcosj, где j - угол между плоскостью колебаний вектора 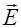в падающей волне и плоскостью поляризатора.

Следовательно, интенсивность света, прошедшего через поляризатор, определяется выражением

j=j_mcos²j. (2.18.1)

Выражение (2.18.1) называется законом Малюса.

Свет, в котором колебания одного направления преобладают над колебаниями других направлений, называется частично поляризованным. Такой свет можно рассматривать как смесь естественного и плоскополяризованного. Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора интенсивность прошедшего света будет изменяться в пределах от j_max до j_min. Степенью поляризации называют выражение

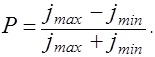(2.18.2)

Из (2.18.2) следует, что для плоскополяризованного света Р =1, а для естественного Р = 0.

При наложении друг на друга двух когерентных плоскополяризованных световых волн, плоскости колебаний вектора 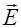, в которых взаимно перпендикулярны, получается волна, в которой вектор 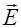изменяется со временем так, что его конец описывает эллипс (рис.2.18.5).

Такой свет называется эллиптическим поляризованным. При разности фаз колебаний, кратной p, эллипс вырождается в прямую и получается плоскополяризованный свет. При разности фаз колебаний, равной нечетному числу , и равенстве амплитуд эллипс превращается в окружность. В этом случае получается свет, поляризованный по кругу(§ 1.7).

В зависимости от направления вращения вектора 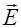различают правую и левую эллиптическую и круговую поляризацию.