Синтез сателлитных механизмов
Зубчатые механизмы с подвижными осями некоторых зубчатых колёс называются сателлитными. Сателлитная передача, в которой на отдельные звенья наложена дополнительная кинематическая связь путём закрепления одного из центральных колёс, называется планетарной, а без дополнительной связи – дифференциальной. Эта связь может быть осуществлена соединением двух его звеньев замыкающей цепью, в результате чего образуется замкнутая дифференциальная передача.
Сателлитные механизмы дают возможность при небольшом количестве колёс, лёгкости и компактности конструкции воспроизводить большие передаточные отношения. Поэтому они получили широкое распространение в машиностроениии и приборостроении. Планетарные механизмы и замкнутые дифференциалы применяются для реализации передаточных отношений, а дифференциалы – для сложения угловых скоростей или разложения независимого вращательного движения двух выходных звеньев механизма.
Существует несколько методов определения передаточных отношений сателлитных механизмов: аналитический, основанный на принципе обращения движения, и графический, с помощью построения треугольников скоростей.
4.2.1. Графоаналитический метод определения
передаточного отношения (способ Л.П. Смирнова)
|
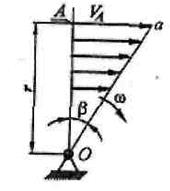
| Рис. 4.10. Треугольники скоростей |
Сущность метода определения передаточного отношения с помощью треугольников скоростей основан на том, что линейная скорость при вращении тела относительно неподвижной оси прямо пропорциональна радиусу вращения (V = ωr), и, следовательно, линейные скорости точек, лежащих на любом радиусе, изменяются по закону прямой линии (рис. 4.10).
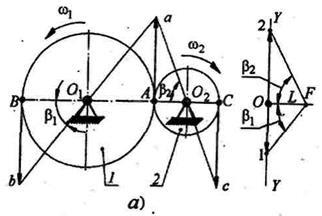
На рис. 4.11 показаны начальные окружности колёс, соприкасающиеся в точке А, линейная скорость VA которых изображается вектором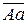 
.
| 
|
| Рис. 4.11. Начальные окружности колёс, соприкасающиеся в точке А |
Для колеса 1 изменение скоростей точек, расположенных на диаметре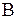 
А, изображается в виде треугольников О1Аа и O1Bb. Для колеса 2 скорости точек, расположенных на диаметре АС, изменяются по закону треугольников:О2Аа и О2Сс.
Длина отрезка Аа на чертеже равна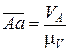 
, отрезка ОА –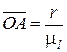 
(рис. 4.10), тогда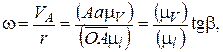 
где μV – масштаб скорости; μl – масштаб длины. Поскольку 
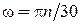, то получим 
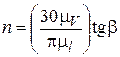. Векторы линейных скоростей точек прямой ОА в масштабе μV ограничиваются наклонной Оа, составляющей угол β с прямой ОА и характеризующей распределение этих скоростей на отрезке ОА.
Следовательно, угловая скорость и число оборотов пропорциональны тангенсу угла с вершиной в точке О. Полученная зависимость позволяет перейти к графическим построениям для определения передаточного отношения механизмов с вращательным движением звеньев.
В зубчатой передаче (рис. 4.11) на плане скоростей наклонные ab и ас составляют углы β1 и β2 с линией центров О1О2 и характеризуют закон изменения линейных скоростей на диаметрах колёс 1 и 2.
Проведём прямую YY перпендикулярно О1O2 и от некоторой точки О на перпендикуляре к YY отложим отрезок произвольной длины OF = L. Затем через точку F проведём лучи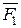 
и 
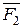параллельно bа и са. Точки 1 и 2 пересечения лучей с прямой YY ограничивают длины отрезков 
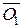и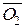 
.
В результате получаем
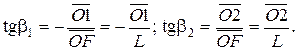
Отсюда
,
,
.
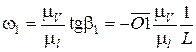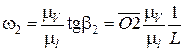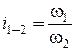Числа оборотов колёс 1 и 2 определяются по зависимостям:
,
.
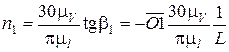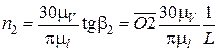Следовательно,
.
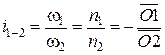Для случая зубчатой передачи с внутренним зацеплением (рис. 4.11, б)
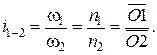
Из изложенного видно, что отрезк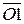и 
и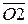 
изображают угловые скорости ω1,2 в масштабе 
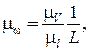а числа оборотов n1,2 в масштабе 
.
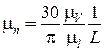Если отрезки на плане угловых скоростей располагаются по разным сторонам от точки О, то колеса вращаются в противоположные стороны: одно – по часовой стрелке, другое – против. Следовательно, передаточное отношение оказывается отрицательным. В случае, когда отрезк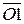и и 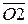лежат по одну сторону от прямой OF, передаточное отношение является положительной величиной.
Планетарные механизмы
Механизмы, включающие неподвижные колёса, называются планетарными (рис. 4.12). Они состоят из центральных колёс 1 и 3, оси которых совпадают, водила Н и сателлита 2 (их может быть несколько). Сателлит вращается относительно своей оси и одновременно обкатывается вокруг колеса 1. Зубья колеса 1 нажимают на зубья колеса 2 и поворачивают его относительно неподвижного (опорного) колеса 3. При этом сателлит нажимает на свою ось и заставляет водило Н вращаться.
|
|
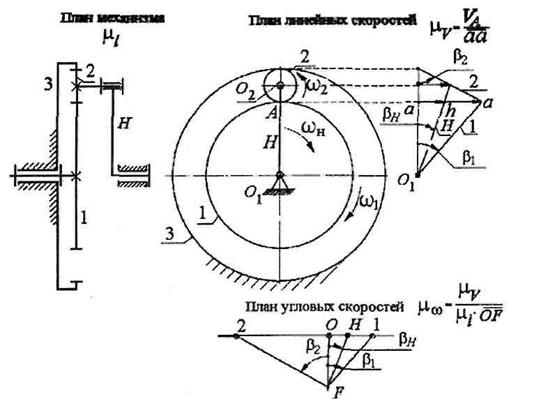
Рис. 4.12. Планетарный механизм
Кинематический анализ планетарных механизмов
Кинематический анализ планетарных механизмов выполняется по методу Виллиса, основанному на остановке водила. Для этого всей планетарной передаче (рис. 4.12) мысленно сообщается вращение с угловой скоростью водила, но направленной в обратную сторону, т.е. – ωН. Таким образом, получается обращенное движение, при котором водило мысленно останавливается, а другие колёса освобождаются. Преобразованный механизм представляет собой рядовой зубчатый механизм, скорость звеньевв котором составляет ωН = 0; ω1(н)=ω1(3) – ωН(3); колесо 3 было неподвижно, а в преобразованном механизме его угловая скорость равнаωН(3).
Верхний индекс показывает неподвижное звено. Мысленная остановка водила равноценна вычитанию его угловой скорости из угловых скоростей подвижных колёс. Передаточное отношение в преобразованном механизме в итоге представляется как
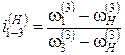. Но поскольку ω3(3) = 0, то получается
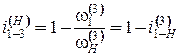, откуда передаточное отношение планетарного механизма будет 
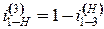. При этом 
.
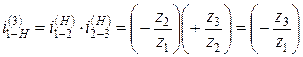В обращенном механизме сателлит 2 является "паразитным" колесом и лишь изменяет направление вращения ведомого колеса. Окончательно будем иметь:
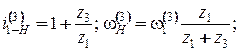
В общем виде формула Виллиса представляется как
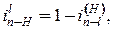
где n и l – центральные колёса. При этом
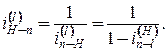
При графическом методе определения передаточных отношений в планетарном механизме строятся планы линейных и угловых скоростей (рис. 4.12). Тогда
.
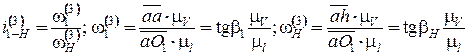Из плана угловых скоростей:
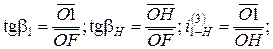
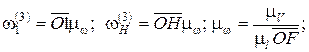
где μω – масштабный коэффициент плана угловых скоростей.
Передаточное отношение i1-н(3) оказывается положительным, так как отрезк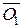и и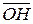 
располагаются по одну и ту же сторону от вертикали OF.
Наиболее распространённые схемы планетарных механизмов
Основные схемы планетарных механизмов представлены на рис. 4.13.
В этих схемах неподвижным колесом может быть колесо 3 либо колесо 1.
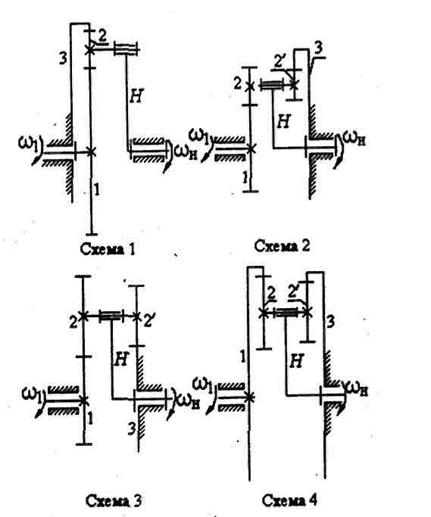
Рис. 4.13. Основные схемы планетарных механизмов
Схема 1. Планетарная передача (Джемса) работает как силовой редуктор, т.е. уменьшает угловую скорость входного звена, если водило является выходным. Передаточное отношение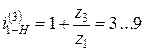 
.
Наименьшие габариты механизм имеет при i1-H(3) = 4. Максимальное передаточное отношение можно получить в случае, когда неподвижным звеном является большое центральное колесо.
Эта передача работает как мультипликатор, т.е. увеличивает угловую скорость, когда входным звеном является водило. Направление угловой скорости входного звена в механизме не изменяется.
Схема 2. Редуктор со сдвоенными сателлитами по габаритам мало отличается от редуктора Джемса при i1-H(3)= 7. Передаточное отношение передачи 
.
Направление вращения выходного звена совпадает с направлением угловой скорости входного колеса.
Схема 3.Редуктор Давида применяется в несиловых передачах, в основном в приборостроении. Передаточное отношение равно
.
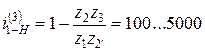Схема 4.Редуктор Давида понижает скорость только при передаче от водила Н к колесу 1. Он имеет меньшие габариты по сравнению со схемой 3, но изготовление колёс с внутренним зацеплением более затруднительно. Передаточное отношение равно
.
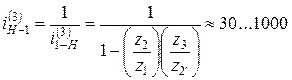В редукторах Давида (схемы 3 и 4) знак передаточного отношения всегда отрицательный, т.е. входное и выходное звенья вращаются в разные стороны.
Выбор чисел зубьев колес планетарной передачи
При назначении чисел зубьев планетарного механизма учитывается ряд ограничений, важнейшие из которых следующие:
· числа зубьев должны быть целыми числами;
· сочетание чисел зубьев колес должно обеспечивать заданное передаточное отношение с допустимой точностью;
· при отсутствии специальных требований в передаче целесообразно использовать нулевые колеса. Это ограничение записывается в форме отсутствия подреза зубьев: z > zmin=17 – для колес с внешними зубьями, нарезанными стандартным инструментом, и z > zmin = 85 при h*a=1 и z > zmin= 58 при h*a = 0,8 – для колес с внутренними зубьями, в зависимости от параметров долбяка;
· для обеспечения движения точек по соосным окружностям оси центральных колес и водила Н должны совпадать между собой (условие соосности);
· при расположении сателлитов в одной плоскости, т.е. без смещения в осевом направлении, соседние сателлиты должны располагаться с таким окружным шагом, чтобы между окружностями вершин обеспечивался гарантированный зазор (условие соседства);
· сборка нескольких сателлитов должна осуществляться без натягов при равных окружных шагах между ними (условие сборки).
Условие правильного зацепления, обусловливающее отсутствие заклинивания и интерференции зубьев, обеспечивается числами зубьев зацепляющихся колес в случае нарезания их долбяком, приведенными в табл. 4.1.
Таблица 4.1
Дата добавления: 2015-07-22; просмотров: 2809;