Топологическая и объектная модели
Для представления пространственно-распределенных данных в цифровом виде используются два основных вида векторных геометрических моделей: бесструктурная (объектная) и топологическая.
Топология определяет наличие связей между пространственными объектами и ее тип. Векторные данные могут содержать информацию о топологии объектов или не содержать. При векторной нетопологической (бесструктурной) форме представления объект отвечает на вопрос «где находится объект?», а при топологической «где находится объект и какие связи с другими объектами он имеет?». Определение топологии осуществляется либо непосредственно на стадии сбора метрической информации, либо после сбора не основе дополнительного анализа и ввода этой информации.
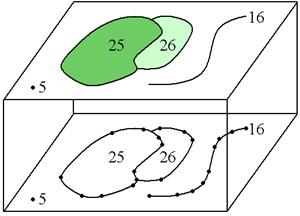
В объектной (бесструктурной) модели объекты делятся на точечные, линейные и площадные, представляемые в виде последовательности координат контура. Такая модель, по сути, переводит «один в один» графическое изображение карты и кажется наиболее естественной и логичной в основном потому, что карта реализуется как умозрительная модель. Каждый примитив отображается одной логической записью, как строки переменной длины пар координат (X,Y). В этой модели соседние области должны иметь разные цепочки для общих сторон. Т.е. не существует областей, для которых какая-либо цепочка записей была бы общей.
|
Структура данных
| Объект | Номер | Положение |
| Точка | Одна пара координат (x,y) | |
| Линия | Набор пар координат (x,y) | |
| Область | Набор пар координат (x,y), первая и последняя совпадают |
Рисунок 8. Спагетти-модель векторных данных.
Каждая сторона каждой области имеет свой уникальный набор линий и пар координат (нет явной топологической информации, модель – прямой перевод графического изображения). Фрагменты общей стороны имеют одинаковые координаты, но записаны они независимо друг от друга. Пространственные отношения между объектами карты, такие как, например, положение смежных областей подразумеваются, но не записываются. В результате отсутствия явного описания таких отношений появляется дополнительная вычислительная нагрузка, которая затрудняет измерения и анализ. Бесструктурная модель применяется в случае, когда нет необходимости в отображении и хранении связей между объектами, либо этих связей попросту не существует. Представление карты в таком виде является эффективным, и как следствие, наиболее применимым методом картографического отображения и зачастую используется в компьютеризированной картографии, где анализ не является главной целью. Следует отметить, что прорисовка таких моделей при выводе на бумажную основу с помощью плоттеров осуществляется значительно быстрее.
Топологические модели – это модели, которые отражают взаимные связи между объектами, не зависящие от геометрических свойств и содержат топологическую информацию в явном виде. Для возможности использования аналитических методов необходимо внести в систему максимальное количество топологических отношений. Топологическая модель данных объединяет решения некоторых из наиболее часто используемых в географическом анализе функций.
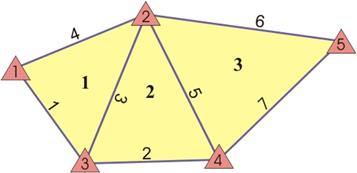
Топологическая структура имеет сложную структуру и содержит базовые элементы – дугу, точку, внутреннюю точку полигона и вспомогательный (связующий) элемент – топологический узел. Узел – это пересечение двух или более дуг, его номер используется для ссылки на любую дугу, которой он принадлежит. В этом случае каждая линия имеет два набора чисел: пары координат промежуточных точек и номера узлов. Схема сочетания элементов показана на рисунке 9.
Модель представляет собой ориентированный граф, где дугами являются контуры объектов, а вершинами топологические узлы. Описание каждой дуги содержит два идентификатора узлов, к которым примыкает дуга, идентификаторы правого и левого полигонов, количество точек в метрике дуги.
Совокупность таких данных для всех объектов карты называют топологической таблицей. Каждая дуга, кроме того, содержит два идентификатора: внутренний, идентифицирующий саму дугу, и пользовательский, описывающий принадлежность дуги к объекту, полигон описывается при помощи внутренней точки, представляющий собой обычный точечный объект, помещенный во внутреннюю область полигона и имеющий идентификатор полигона.
| Файл узлов | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Номер узла | Координата Х | Координата Y | |||||||||||||||||||||||||||||||||||||||||||||||
| Файл областей | Файл дуг | |||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
Рисунок 9. Топологическая модель векторных данных
Метрика формируется на основе идентификатора его внутренней области путем так называемого процесса сборки. После выполнения этого процесса получаем список дуг (таблица сборки) из которых состоит полигон. Сборку необходимо воспроизводить после каждого редактирования метрических данных, поскольку в процессе редактирования сформированная система полигонов разрушается. В геоинформационных системах последнего поколения (ARCGIS) процесс сборки полигонов после редактирования его границ производится автоматически.
Следует отметить особенность так называемых физических структур цифровых карт. Цифровые карты являются программно-зависимыми, т.е. конкретная физическая структура, созданная при помощи одного программного средства ГИС, не сможет функционировать под управлением другого программного средства без операции конвертирования над данными. В процессе конвертирования данных часто происходит искажение или полная потеря топологических отношений. Важное значение процесса сборки топологии состоит в том, что во время ее выполнения осуществляется контроль корректности формирования цифровой карты.
Построение топологической структуры важно для построения многослойной модели. В геоинформационных системах топологическая модель определяется наличием следующих характеристик:
связанностью объектов – векторы должны храниться не как независимые наборы точек, а как взаимосвязанные друг с другом объекты (линейный объект реки связан с полигональным объектом водоема, в который река впадает);
дублирующие дуги копируются, а не вводятся дважды;
полигоны собираются из дуг и должны быть замкнуты;
дуги соединяются в узлах;
связанность и примыкание районов – информация о взаимном расположении районов и узлах пересечения районов (линия дороги является границей административных районов)
пересечение – информация о типах пересечений (дорога и мост, две дороги)
близость – показатель пространственной близости линейных или полигональных объектов, которая оценивается числовым параметром.
Топологическая модель применяется в случаях, если для решения задачи требуется знание о топологических отношениях.
Достоинство топологической модели состоит в том, что оно максимально полно описывает моделируемую территорию, поскольку содержит описание, как метрической информации, так и топологических отношений.
Топологическое представление имеет ряд недостатков:
разрушение сформированной системы полигонов в процессе редактирования и необходимость процесса сборки для ее восстановления;
продолжительность создания топологической модели в 1,5-2 раза больше, чем при создании бесструктурной модели;
создание адекватной для различных ситуаций модели должен проводить специалист, владеющий принципами моделирования.
Векторная модель - строится на векторах, занимающих часть пространства, в отличие от занимающих все пространство растровыхмоделей. Это определяет их основное преимущество - требование меньшей памяти для хранения и меньших затрат времени на обработку. Векторной форма представления дает возможности доступного манипулирования и редактирования данными. Векторная модель может организовывать пространство в любой последовательности и дает произвольный доступ к данным. Кроме того, удобнее использовать некоторые элементарные множества точек, поддающиеся формальным преобразованиям, в векторной форме легче осуществляются операции с линейными и точечными объектами, например анализ сетей. Несомненным преимуществом векторного представления данных является более высокая точность их пространственного определения, которая ограничивается возможностями метода внутреннего представления координат (8 или 16 десятичных знаков). Только некоторые классы данных, получаемые в процессе измерений, соответствуют точности векторных данных. Понижение точности представления реальных данных в векторной модели никак не обусловлено формой их представления. Обычно линии на карте имеют точность примерно 0.5мм и именно это значение отражает неопределенность положения объекта. Понижение точности часто происходит из-за невозможности точного отображения действительности. Не все природные явления имеют четкие границы, которые можно представить в виде математически определенных линий. Это обусловлено динамикой явлений или способами сбора пространственной информации.
Большинство современных геоинформационных систем поддерживают работу как с векторными моделями, так и с растровыми. Векторные данные используются для представления информации, которая имеет объектную природу и нуждается в манипулировании и пространственном анализе. Растровое представление данных в ГИС используется в качестве растровой подложки для создания векторной модели.
Для анализа и обработки в ГИС также используется растровое или матричное представление данных.
Каким же образом осуществляется описание географических данных в пространстве?
Дата добавления: 2015-07-06; просмотров: 1813;
