Картографические проекции
Использование результатов топографо-геодезических работ существенно упрощаются, если эти результаты отнесены к простейшей – прямоугольной системе координат на плоскости. В такой системе координат многие геодезические задачи на небольших участках местности и на картах решаются путем применения простых формул аналитической геометрии на плоскости. Закон изображения одной поверхности на другой называют проекцией. Картографические проекции основаны на формировании специфического отображения параллелей широты и меридианов долготы эллипсоида на некоторую выравниваемую или развертываемую поверхность. В геометрии, как известно, наиболее простыми развертываемыми поверхностями являются плоскость, цилиндр и конус. Это и определило три семейства картографических проекций: азимутальные, цилиндрические и конические. Независимо от выбранного типа преобразований, любое отображение криволинейной поверхности на плоскость влечет за собой ошибки и искажения. Для геодезических проекций предпочитают проекции, обеспечивающие медленное нарастание в них искажений элементов геодезических построений при постепенном увеличении площади проектируемой территории. Особенно важным является требование, чтобы в проекции обеспечивалась высокая точность и удобство учета этих искажений, причем по наиболее простым формулам. Ошибки проекционных преобразований возникают исходя из точности по четырем характеристикам:
- равноугольность – истинность формы любого объекта;
- равновеликость – равенство площадей;
- равнопромежуточность – истинность измерения расстояний;
- истинность направлений.
Ни одна из картографических проекций не может обеспечить точность отображений на плоскости по всем перечисленным характеристикам.
По характеру искажений картографические проекции подразделяются на равноугольные, равновеликие и произвольные (в частных случаях равнопромежуточные).
Равноугольными (конформными) проекциями называют такие, в которых отсутствуют искажения углов и азимутов линейных элементов. Эти проекции сохраняют без искажений углы (например, между севером и востоком всегда угол должен быть прямым) и формы малых объектов, но в них резко деформируются длины и площади. Следует отметить, что сохранение углов для больших территорий труднодостижимо, и этого можно добиться только на небольших участках.
Равновеликими (равноплощадными) проекциями называют проекции, в которых площади соответствующих областей на поверхности эллипсоидов и на плоскости тождественно равны (пропорциональны). В этих проекциях искажены углы и формы объектов.
Произвольные проекции имеют искажения углов, площадей и длин, но эти искажения распределены по карте таким образом, что они минимальны в центральной части и возрастают на периферии. Частным случаем произвольных проекций являются равнопромежуточные (эквидистантные), в которых искажения длин отсутствуют по одному из направлений: вдоль меридиана или вдоль параллели.
Равнопромежуточныминазывают проекции, сохраняющие длину по одному из главных направлений. Как правило, это проекции с ортогональной картографической сеткой. В этих случаях главными являются направления вдоль меридманов и параллелей. Соответственно определяются равнопромежуточные проекции вдоль одного из направлений. Второй способ построения таких проекций заключается в сохранении единичного масштабного коэффициента вдоль всех направлений из одной точки, либо из двух. Расстояния, измеренные из таких точек, будут точно соответствовать реальным, но для любых других точек это правило не будет действовать. В случае выбора такого вида проекции очень важен выбор точек. Обычно предпочтение отдают точкам, из которых производится наибольшее количество измерений.
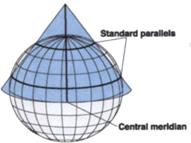а) конические
| 
|
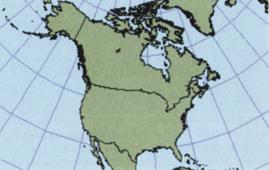
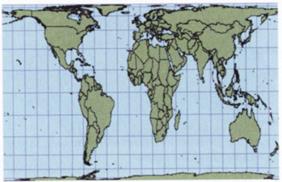
б) цилиндрические
| 
|
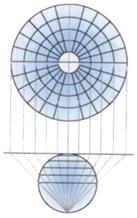в) азимутальные
| 
|
Рисунок 11. Классы проекций по способу построения
Равноазимутальные проекции чаще всего используются в навигации, т.е. когда наибольший интерес представляет сохранение направлений. Аналогично равновеликой проекции, сохранение истинных направлений возможно лишь для одной или двух определенных точек. Прямые линии, проведенные только из этих точек, будут соответствовать истинным направлениям.
По способу построения (развертывания поверхности на плоскость) выделяют три больших класса проекций: конические (а), цилиндрические (б) и азимутальные (в).
Конические проекции образуются на основе проектирования земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно эллипсоида. В прямых конических проекциях оси земного шара и конуса совпадают, при этом выбирается секущий или касательный конус. После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость. В зависимости от размеров изображаемой площади в конических проекциях принимаются одна или две параллели, вдоль которых сохраняются длины без искажений. Одна параллель (касательная) принимается при небольшом протяжении по широте: две параллели (секущие) при большом протяжении для уменьшения отклонений масштабов от единицы. Такие параллели называют стандартными. Особенностью конических проекций является то, что их центральные линии совпадают со средними параллелями. Следовательно, конические проекции удобны для изображения территорий, расположенных в средних широтах и значительно вытянутых по долготе. Именно поэтому многие карты бывшего Советского Союза составлены в этих проекциях.
Цилиндрические проекцииобразуются на основе проектирования земной поверхности на боковую поверхность цилиндра, определенным образом ориентированного относительно земного эллипсоида. В прямых цилиндрических проекциях параллели и меридианы изображены двумя семействами прямых параллельных линий, перпендикулярных друг другу. Таким образом, задается прямоугольная сетка цилиндрических проекций. Цилиндрические проекции можно рассматривать как частный случай конических, когда вершина конуса отнесена в бесконечность (a=0). Существуют разные способы образования цилиндрических проекций. Цилиндр может быть касательным к эллипсоиду или секущим его. В случае использования касательного цилиндра точность измерения длин выдержана по экватору. Если используется секущий цилиндр – по двум стандартным параллелям, симметричным относительно экватора. Применяются прямые, косые и поперечные цилиндрические проекции, в зависимости от расположения изображаемой области. Цилиндрические проекции применяют при составлении карт мелких и крупных масштабов.
Азимутальные проекции образуются путем проектирования земной поверхности на некоторую плоскость, определенным образом ориентированную относительно эллипсоида. В них параллели изображаются концентрическими окружностями, а меридианы – пучком прямых, исходящих из центра окружности. Углы между меридианами проекций равны соответствующим разностям долгот. Промежутки между параллелями определяются принятым характером изображения (равноугольным или другим). Нормальная сетка проекции ортогональна. Азимутальные проекции можно рассматривать как частный случай конических проекций, в которых a=1.
Применяются прямые, косые и поперечные азимутальные проекции, что определяется широтой центральной точки проекции, выбор которой, в свою очередь, зависит от расположения территории. В зависимости от искажений азимутальные проекции подразделяются как равноугольные, равновеликие и с промежуточными свойствами.
Существует большое разнообразие проекций: псевдоцилиндрические, поликонические, псевдоазимутальные и другие. От правильного выбора картографической проекции зависит возможность условий оптимального решения поставленных задач. Выбор проекций обусловлен многими факторами, которые условно можно объединить в три группы.
Первая группа факторов характеризует объект картографирования с точки зрения географического положения исследуемой территории, ее размеров, конфигурации, значимости отдельных ее частей.
Вторая группа включает факторы, характеризуемые создаваемую карту. В эту группу входят содержание и назначение карты в целом, способы и условия ее использования при решении задач ГИС, требования к точности их решения.
К третьей группе относятся факторы, которые характеризуют получаемую картографическую проекцию. Это условие обеспечения минимума искажений, допустимые максимальные величины искажений, характер их распределения, кривизна изображения меридианов и параллелей.
Выбор картографических проекций предлагается осуществлять в два этапа.
На первом этапе устанавливается совокупность проекций с учетом факторов первой и второй групп. При этом необходимо чтобы центральные линии или точки проекций, вблизи которых масштабы мало изменяются, находились в центре исследуемой территории, а центральные линии совпадали, по возможности, с направлением наибольшего распространения этих территорий. На втором этапе определяют искомую проекцию.
Рассмотрим выбор различных проекций в зависимости от расположения исследуемой территории. Азимутальные проекции выбирают, как правило, для изображения территорий полярных областей. Цилиндрические проекции предпочтительны для территорий, расположенных вблизи и симметрично относительно экватора и вытянутых по долготе. Конические проекции следует использовать для таких же территорий, но не симметричных относительно экватора или расположенных в средних широтах.
Для всех проекций выбранной совокупности по формулам математической картографии вычисляют частные масштабы и искажения. Предпочтение следует отдать, естественно, той проекции, которая имеет наименьшие искажения, более простой вид картографической сетки, а при равных условиях – более простой математический аппарат проекции. Рассматривая возможность использования равновеликих проекций, следует учитывать размер интересующей площади, а также величину и распределение угловых искажений, Небольшие участки отображаются с гораздо меньшими угловыми искажениями при использовании равновеликих проекций, что может быть полезно, когда значение имеют площадь и формы объектов. В случае, когда решают задачу определения наикратчайших расстояний лучше использовать проекции, не искажающие направления. Выбор проекции – один из основных процессов создания ГИС.
При решении задач картографирования в недропользовании на территории России наиболее часто используются две проекции, описанные ниже.
Видоизмененная простая поликоническая проекция применяется как многогранная, т.е. каждый лист определяется в своем варианте проекции.
Рисунок12. Номенклатурные трапеции листов масштаба 1:200000 в поликонической проекции
Особенности видоизмененной простой поликонической проекции и распределение искажений в пределах отдельных листов миллионного масштаба следующие:
- все меридианы изображаются прямыми линиями, отсутствуют искажения длин на крайних параллелях и на меридианах, отстоящих от среднего на ±2º,
- крайние параллели каждого листа (северная и южная) являются дугами окружностей, центры этих параллелей находятся на среднем меридиане, длина их не искажается, средние параллели определяются пропорциональным делением по широте вдоль прямолинейных меридианов,
Земная поверхность, принимаемая за поверхность эллипсоида, делится линиями меридианов и параллелей на трапеции. Трапеции изображаются на отдельных листах в одной и той же проекции (для карты масштаба 1 : 1 000 000 в видоизмененной простой поликонической). Листы Международной карты мира масштаба 1 : 1 000 000 имеют определенные размеры трапеций – по меридианам 4 градуса, по параллелям 6 градусов; на широте от 60 до 76 градуса листы сдваивают, они имеют размеры по параллелям 12; выше 76 градуса объединяют четыре листа и их размер по параллелям составляет 24 градуса.
Применение проекции как многогранной неизбежно связано с введением номенклатуры, т.е. системы обозначения отдельных листов. Для карты миллионного масштаба принято обозначение трапеций по широтным поясам, где в направлении от экватора к полюсам обозначение осуществляется буквами латинского алфавита (A,B,C и т.д.) и по колоннам арабскими цифрами, которые считают от меридиана с долготой 180 (по Гринвичу) против часовой стрелки. Лист, на котором расположен г. Екатеринбург, например, имеет номенклатуру О-41.
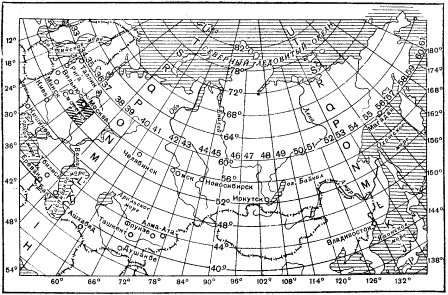
Рисунок 13. Номенклатурное деление территории России
Достоинством видоизмененной простой поликонической проекции, примененной как многогранная, является небольшая величина искажений. Анализ в пределах листа карты показал, что искажения длин не превышают 0.10%, площади 0.15%, углов 5´ и являются практически не ощутимыми. Недостатком этой проекции считают появление разрывов при соединении листов по меридианам и параллелям.
Конформная (равноугольная) псевдоцилиндрическая проекция Гаусса-Крюгера. Для применения такой проекции поверхность земного эллипсоида делят на зоны, заключенные между двумя меридианами с разностью долгот 6 или 3 градуса. Меридианы и параллели изображаются кривыми, симметричными относительно осевого меридиана зоны и экватора. Осевые меридианы шестиградусных зон совпадают с центральными меридианами листов карты масштаба 1 : 1 000 000. Порядковый номер определяется по формуле
n = N-30,
где N – номер колонны листа карты масштаба 1 : 1 000 000.
Долготы осевых меридианов шестиградусных зон определяются по формуле
L0 = 6n – 3, где n - номер зоны.
Прямоугольные координаты x и y в пределах зоны вычисляются относительно экватора и осевого меридиана, которые изображаются прямыми линиями
|
В пределах территории бывшего СССР абсциссы координат Гаусса-Крюгера положительные; ординаты положительные к востоку, отрицательные к западу от осевого меридиана. Чтобы избежать отрицательных значений ординат, точкам осевого меридиана условно придают значение y = 500 000 м с обязательным указанием впереди номера соответствующей зоны. Например, если точка находится в зоне с номером 11 в 25 075м к востоку от осевого меридиана, то значение ее ординаты записывается так: y = 11 525 075 м: если точка расположена к западу от осевого меридиана этой зоны на таком же расстоянии, то y = 11 474 925 м.
В конформной проекции углы треугольников триангуляции не искажаются, т.е. остаются такими же, как на поверхности земного эллипсоида. Масштаб изображения линейных элементов на плоскости постоянен в данной точке и не зависит от азимута этих элементов: линейные искажения на осевом меридиане равны нулю и постепенно возрастают по мере удаления от него: на краю шестиградусной зоны они достигают максимальной величины.
Во странах западного полушария применяют для составления топографических карт универсальную поперечно-цилиндрическую проекцию Меркатора (UTM) в шестиградусных зонах. Эта проекция близка по своим свойствам и распределению искажений к проекции Гаусса-Крюгера, но на осевом меридиане каждой зоны масштаб m=0.9996, а не единица. Проекция UTM получается двойным проектированием - эллипсоида на шар, а затем шара на плоскость в проекции Меркатора.
Рисунок 15. Преобразование координат в геоинформационных системах
Наличие в ГИС программного обеспечения, осуществляющего проекционные преобразования, позволяет легко перевести данные из одной проекции в другую. Такое бывает необходимо, если полученные исходные данные существуют в проекции, не совпадающей с выбранной в вашем проекте или нужно изменить проекцию данных проекта для решения какой-либо специфической задачи. Переход из одной проекции в другую носит название проекционных преобразований. Существует возможность перевода координат цифровых данных, изначально введенных в условных координатах дигитайзера или растровой подложки с помощью преобразований плоскости.
Каждый пространственный объект кроме пространственной привязки обладает некоторой содержательной сущностью, и в следующей главе рассмотрим возможности описания ее.
Дата добавления: 2015-07-06; просмотров: 3262;