Порядок
Если s — копия начального отрезка t, то можно найти такое продолжение и последовательности s, что s^и = t. Определим отношение порядка
s  t = ($u.s^и = t)
t = ($u.s^и = t)
и будем говорить, что s является префиксом t. Например:<х, у>  <х, у, z>. Отношение
<х, у, z>. Отношение  является частичным упорядочением и имеет своим наименьшим элементом <>. Об этом говорят законы
является частичным упорядочением и имеет своим наименьшим элементом <>. Об этом говорят законы
L1.<>  s наименьший элемент.
s наименьший элемент.
L2.s  s рефлексивность.
s рефлексивность.
L3.s  t AND t
t AND t  s
s 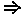 t = sантисимметричность.
t = sантисимметричность.
L4.s  t AND t
t AND t  u
u 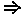 s
s  uтранзитивность.
uтранзитивность.
Следующий закон вместе сL1 позволяет определить, является ли справедливым отношение s  t:
t:
L5.(<x>^s)  t ºt
t ºt 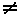 <> AND x= t0 AND s
<> AND x= t0 AND s  t’.
t’.
Будем говорить, что функция f из множества протоколов во множество протоколов монотонна, если она сохраняет отношение порядка  , т. е. f(s)
, т. е. f(s)  f(t) всякий раз, когда s
f(t) всякий раз, когда s  t.
t.
Длина
Длину протокола t будем обозначать #t. Например, #<х, у, z> = 3.
Следующие законы определяют операцию #:
L1.#<> = 0.
L2.#<x> = 1.
L3.#(s ^t) = #s + #t.
Число вхождений символа х в протокол s определяется как:
s ¯ х = #(s{х}).
Дата добавления: 2015-07-18; просмотров: 642;
