Протоколы процесса

Понятие протокола введено, как последовательная запись поведения процесса вплоть до некоторого момента времени. До начала процесса неизвестно, какой именно из возможных протоколов будет реализован: его выбор зависит от внешних по отношению к процессу факторов. Однако полный набор всех возможных протоколов процесса Р может быть известен заранее. Введем функцию протоколы(Р) для обозначения этого множества.

Пример 3.11. Единственным протоколом процесса СТОП является <>:

протоколы(СТОП) = {<>}.

Пример 3.12. протоколы(ЧАСЫ) = {<>, <тик>, <тик, тик>,…} = {тик}^*. Здесь множество протоколов бесконечно.

Законы

В этом разделе покажем, как вычислить множество протоколов процесса, определенного с помощью уже введенных обозначений.

L1.протоколы(СТОП) = {t | t = <>} = {<>}.

Протокол процесса (с Р) может быть пустым, поскольку <> является протоколом поведения любого процесса до момента наступления его первого события.

L2. протоколы(с Р) = {t | t = <> OR (t₀ = c AND t' протоколы(Р))}

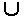= {<> {<c>^t | t протоколы(Р)}.

Эти два закона можно объединить в один общий закон, которому подчиняется конструкция выбора:

L3.протоколы(x: B Р(x)) =

= {t | t = <> OR (t₀ В AND t' протоколы(Р(t₀)))}.

Несколько сложнее найти множество протоколов рекурсивно определенного процесса, который является решением уравнения Х = F(Х).

L4.протоколы(mХ: А.F(Х)) = 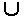_n³0 протоколы(Fⁿ(СТОП_A)).

Пример 3.13. протоколы(ТАП) = 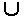_n³0 {s | s <мон, шок>ⁿ}.

Доказательство.

1) Согласно предположению индукции

протоколы(Fⁿ(ТAП)) = {t | t <мон, шок>ⁿ},

где F(X) = (мон шок X).

2) протоколы(F⁰(СТОП)) = {<>} = {s | s <мон, шок>⁰}, для n = 0 предположение выполняется.

3) Покажем, что предположение также справедливо для n+1:

протоколы(Fⁿ⁺¹(СТОП)) = протоколы(мон шок Fⁿ(СТОП)) =

= {<>, <мон>} 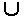{<мон, шок>^t | t протоколы(Fⁿ(СТОП))} =

= {<>, {<мон>} 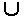{<мон, шок>^t | t <мон, шок>ⁿ} =

= {s | s = <> OR s = <мон> OR $t.s = <мон, шок>^t AND t <мон, шок>ⁿ}

= {s | s <мон, шок>ⁿ⁺¹}.

Справедливо, что <> является протоколом любого процесса до момента наступления его первого события. Кроме того, если (s^t) – протокол процесса до некоторого момента, то s должен быть протоколом того же процесса до некоторого более раннего момента времени. Наконец, каждое происходящее событие должно содержаться в алфавите процесса. Три этих факта находят свое формальное выражение в следующих законах:

L5.<> протоколы(P).

L6.s^t протоколы(P) 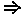s протоколы(P).

L7.протоколы(P) 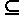{aP}^*.

После

Если s протоколы(P), то P/s (P после s) – это процесс, ведущий себя так, как ведет себя Р с момента завершения всех действий, записанных в протоколе s. Если s не является протоколом P, то P/s не определено.

Пример 3.14.(ТАП / <мон>) = (шок → ТАП).