Использование высказываний в программах

Высказывания используются для доказательства правильности программ. Тогда высказывания необходимо формулировать в некоторой формальной логической системе. Обычно используется исчисление предикатов первого порядка.

Исчисление - это метод или процесс рассуждений посредством вычислений над символами. В исчислении предикатов высказывания являются логическими переменными или выражениями, имеющими значение T - истина или F - ложь. Наша цель - при написании программы некоторым способом доказать истинность высказывания (2.2) - триады Хоара {Q} S {R}. Для этого нужно уметь записывать его в исчислении предикатов и формально доказывать его истинность.

Предикат, помещенный в программу, был нами назван высказыванием. Утверждается, что он истинен в соответствующий момент выполнения программы. В предусловии Q нужно отражать тот факт, что входные переменные получили начальные значения. Для обозначения начальных значений будем использовать большие буквы.

Пример 2.8. Пусть надо определить приближенное значение квадратного корня: s = sqrt(n), где n, s Nat. Определим постусловие в виде:

R: s×s n < (s+1)×(s+1).

Пример 2.9. Даны целочисленные n > 0 и массив a[1,...,n]. Отсортировать массив, т.е. установить

R: (" i: 1 i < n: a[i] a[i+1]).

Пример 2.10. Определить x как максимальное значение массива a[1,...,n]. Определим постусловие:

R: {x = max({y | y 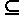a})}.

Для построения программы следует определить математическое понятие max. Тогда

R: {($ i: 1 i n: x = a[i]) AND (" i: 1 i n: a[i] = x)}.

Пример 2.11. Пусть имеем программу S обмена значениями двух целых переменных a и b. Сформулируем входное и выходное высказывания программы и представим программу S в виде предиката:

{a = A AND b = B} S {a = B AND b = A},(2.4)

где A, B - конкретные значения переменных a, b.

Программа вместе с высказываниями между каждой парой соседних операторов называется наброском доказательства. Последовательно, для каждого оператора программы формулируя предикат (2.4), можно доказать, что программа удовлетворяет своим спецификациям. Представим набросок доказательства для программы S:

{a = A AND b = B};

r := a; {r = a AND a = A AND b = B};

a := b; {r = a ANDa = B AND b = B};

b := r; {a = B AND b = A}.

Не обязательно набросок доказательства должен быть настолько полным. Для документирования программы нужно вставить достаточно высказываний, чтобы программа стала понимаемой.

Программа, содержащая высказывания для ее документирования, называется аннотированной программой. Чтобы использовать высказывания для доказательства правильности программы, необходимы соответствующие правила верификации.